Tính Diện Tích Hình Bình Hành Online Dễ Dàng, Chính Xác, Công Thức Chuẩn

Hình bình hành là một trong những hình học phẳng cơ bản trong môn hình học. Đây là loại hình có rất nhiều ứng dụng trong thực tiễn cũng như trong các bài toán hình học. Trong bài viết này, chúng ta sẽ cùng tìm hiểu về diện tích của hình bình hành, định nghĩa, công thức tính, cũng như một số bài tập từ cơ bản đến nâng cao để củng cố kiến thức.

Định Nghĩa Hình Bình Hành

Hình bình hành là một bốn cạnh (tứ giác) có hai cặp cạnh đối diện song song và bằng nhau. Các góc đối diện của hình bình hành cũng bằng nhau. Nếu bạn nhìn vào hình bình hành, bạn sẽ thấy rằng việc cắt nó theo đường chéo sẽ tạo ra hai tam giác đều nhau.

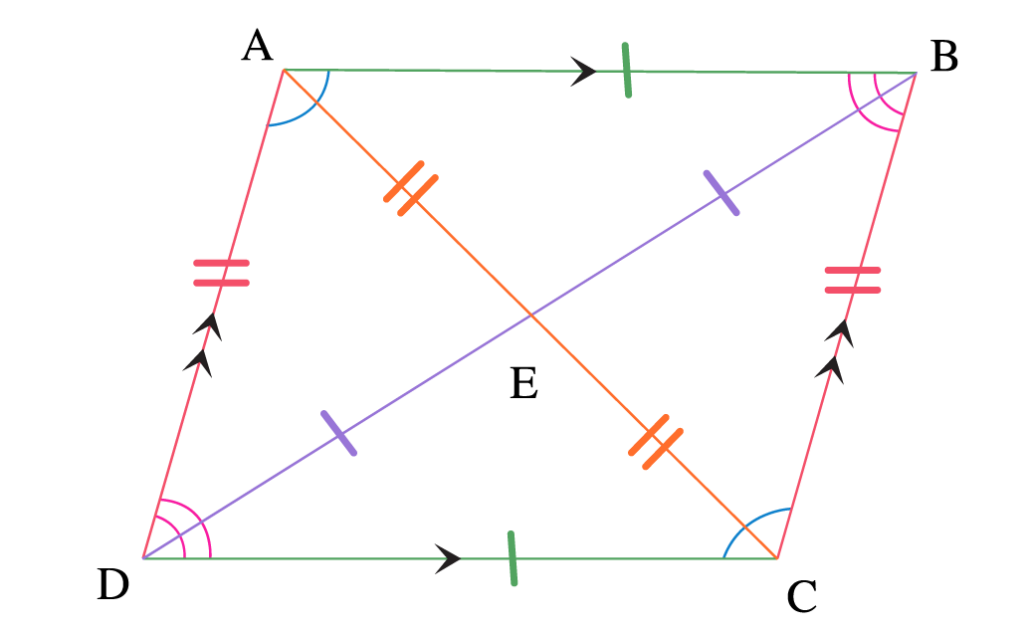
Đặc điểm nổi bật của hình bình hành là:

– Hai cặp cạnh đối diện vừa song song vừa bằng nhau.
– Hai góc đối diện bằng nhau.
– Tổng của hai góc kề bên là 180 độ.

Công Thức Tính Diện Tích Hình Bình Hành

Diện tích của hình bình hành có thể được tính bằng công thức:

\text{Diện tích} = a \times h

Trong đó:
– a là chiều dài đáy (một trong hai cạnh song song của hình bình hành).
– h là chiều cao (khoảng cách vuông góc từ đỉnh này xuống đường thẳng của đáy đối diện).

Ngoài ra, diện tích của hình bình hành cũng có thể tính bằng công thức liên quan đến độ dài của hai đường chéo và góc giữa chúng, nhưng công thức này ít được sử dụng hơn trong thực tiễn.

Một Vài Bài Tập Tính Diện Tích Hình Bình Hành

Để hiểu rõ hơn về cách tính diện tích của hình bình hành, chúng ta sẽ cùng thử sức với một số bài tập từ cơ bản đến nâng cao.

Bài Tập 1: Tính Diện Tích Cơ Bản

Cho hình bình hành có chiều dài đáy là 8 cm và chiều cao là 5 cm. Tính diện tích của hình bình hành.

Giải:

Áp dụng công thức tính diện tích:

\text{Diện tích} = a \times h = 8 \times 5 = 40 \text{ cm}^2

Vậy diện tích của hình bình hành là 40 cm².

Bài Tập 2: Tính Diện Tích Khi Biết Cạnh và Góc

Cho một hình bình hành có độ dài cạnh là 6 cm và góc giữa hai cạnh là 60 độ. Tính diện tích của hình bình hành.

Giải:

Đầu tiên, cần tìm ra chiều cao h :

h = a \times sin(\theta) = 6 \times sin(60^\circ) = 6 \times \frac{\sqrt{3}}{2} = 3\sqrt{3}

Sau đó, áp dụng công thức tính diện tích:

\text{Diện tích} = a \times h = 6 \times 3\sqrt{3} = 18\sqrt{3} \text{ cm}^2

Bài Tập 3: Bài Tập Nâng Cao

Cho hình bình hành có hai đường chéo dài 10 cm và 12 cm, và góc giữa hai đường chéo là 30 độ. Tính diện tích của hình bình hành.

Giải:

Sử dụng công thức diện tích theo đường chéo và góc:

\text{Diện tích} = \frac{1}{2} \times d_1 \times d_2 \times sin(\theta)

Trong đó:
– d_1 = 10 \text{ cm}
– d_2 = 12 \text{ cm}
– \theta = 30^\circ

Tính diện tích:

\text{Diện tích} = \frac{1}{2} \times 10 \times 12 \times sin(30^\circ) = \frac{1}{2} \times 10 \times 12 \times \frac{1}{2} = 30 \text{ cm}^2

Vậy diện tích của hình bình hành này là 30 cm².

Kết Luận

Diện tích của hình bình hành là một trong những khái niệm cơ bản trong hình học. Với công thức đơn giản a \times h , chúng ta có thể dễ dàng tính toán diện tích cho nhiều bài toán khác nhau. Bài tập từ cơ bản đến nâng cao đã giúp người học có cái nhìn sâu sắc hơn về hình bình hành và ứng dụng của nó trong thực tiễn.

Hy vọng rằng qua bài viết này, các bạn đã có thêm kiến thức về diện tích của hình bình hành và có thể áp dụng vào các bài tập thực tế. Hãy thường xuyên luyện tập để nâng cao kỹ năng toán học của mình!