Tính Diện Tích Bề Mặt Cong Bán Cầu Online – Công Thức Chuẩn

Bán cầu là một trong những hình khối cơ bản trong hình học không gian. Trong thực tiễn, nó là một phần của hình cầu, được xác định bởi bán kính và mặt phẳng cắt qua tâm hình cầu. Diện tích bề mặt cong của bán cầu là một chủ đề quan trọng trong Toán học, đặc biệt là khi nghiên cứu về các hình khối 3D. Trong bài viết này, chúng ta sẽ tìm hiểu về định nghĩa, công thức tính diện tích bề mặt cong của bán cầu, và làm một số bài tập từ cơ bản đến nâng cao.

Định Nghĩa Bán Cầu

Bán cầu là một nửa của hình cầu. Một bán cầu có thể được hình dung là hình cầu được cắt bởi mặt phẳng đi qua tâm của nó. Bán cầu bao gồm cả mặt cong và mặt đáy. Mặt cong của bán cầu có diện tích mà chúng ta sẽ tính toán, trong khi mặt đáy là hình tròn có diện tích riêng.

Công Thức Tính Diện Tích Bề Mặt Cong của Bán Cầu

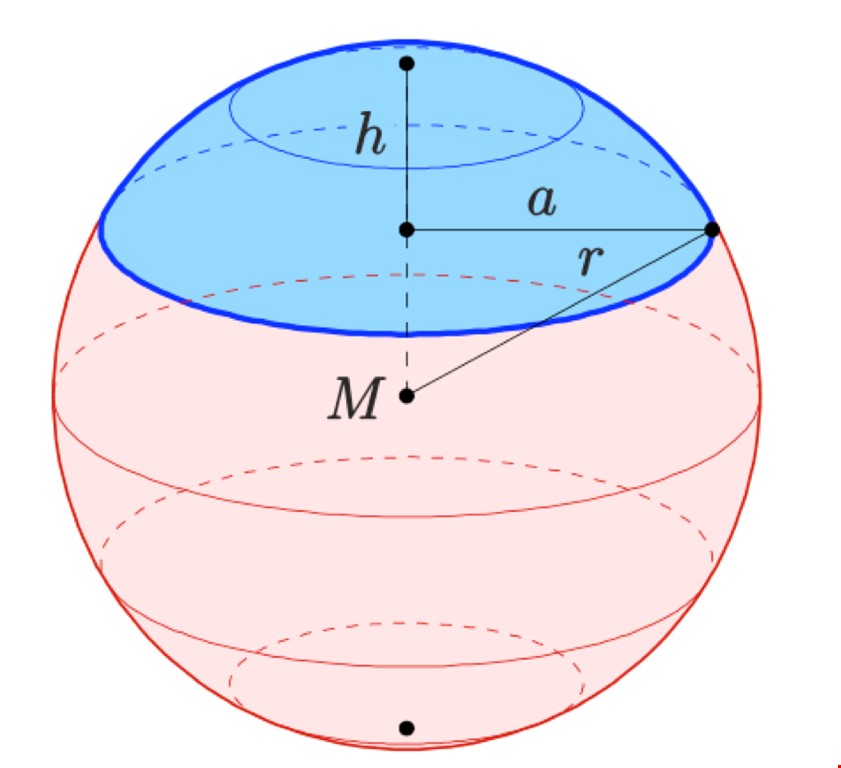
Diện tích bề mặt cong của bán cầu được tính bằng công thức sau:

S_{bán cầu} = 2\pi r^2

Trong đó:
– S_{bán cầu} là diện tích bề mặt cong của bán cầu.
– r là bán kính của bán cầu.
– \pi là hằng số Pi (khoảng 3.14159).

Ngoài ra, nếu tính cả diện tích mặt đáy (hình tròn) của bán cầu, công thức tổng thể sẽ là:

S_{tổng} = 2\pi r^2 + \pi r^2 = 3\pi r^2

Trên công thức này:
– S_{tổng} là tổng diện tích bề mặt của bán cầu bao gồm cả mặt cong và mặt đáy.

Ví Dụ Tính Diện Tích Bề Mặt Cong Bán Cầu

Bài Tập 1: Diện Tích Bề Mặt Cong Của Bán Cầu Với Bán Kính Bằng 3

Đề bài: Tính diện tích bề mặt cong của bán cầu có bán kính r = 3 cm.

Giải:
Áp dụng công thức tính diện tích bề mặt cong:

S_{bán cầu} = 2\pi r^2 = 2\pi \cdot 3^2 = 2\pi \times 9 = 18\pi \approx 56.55 \text{ cm}^2

Vậy diện tích bề mặt cong của bán cầu là khoảng 56.55 cm².

Bài Tập 2: Tính Diện Tích Bề Mặt Tổng Của Bán Cầu

Đề bài: Tính tổng diện tích bề mặt của bán cầu với bán kính r = 4 cm.

Giải:
Áp dụng công thức tổng diện tích bề mặt:

S_{tổng} = 3\pi r^2 = 3\pi \cdot 4^2 = 3\pi \times 16 = 48\pi \approx 150.80 \text{ cm}^2

Vậy tổng diện tích bề mặt của bán cầu là khoảng 150.80 cm².

Bài Tập Nâng Cao: Tìm Bán Kính Qua Diện Tích Bề Mặt Cong

Bài Tập 3: Tìm Bán Kính Của Bán Cầu Với Diện Tích Bề Mặt Cong Là 50 cm²

Đề bài: Nếu diện tích bề mặt cong của một bán cầu là 50 cm², hãy tìm bán kính của nó.

Giải:
Sử dụng công thức:

S_{bán cầu} = 2\pi r^2 \Rightarrow 50 = 2\pi r^2

Giải phương trình này:

r^2 = \frac{50}{2\pi} = \frac{25}{\pi} r = \sqrt{\frac{25}{\pi}} \approx \frac{5}{\sqrt{\pi}} \approx 2.83 \text{ cm}

Vậy bán kính của bán cầu là khoảng 2.83 cm.

Kết Luận

Tính toán diện tích bề mặt cong của bán cầu là một bài toán thú vị và hữu ích trong hình học. Qua bài viết này, chúng ta đã tìm hiểu định nghĩa, công thức tính và đã giải quyết một số bài tập từ cơ bản đến nâng cao. Hi vọng rằng những kiến thức này sẽ giúp các bạn củng cố và mở rộng thêm sự hiểu biết về hình học không gian. Hãy thử sức với các bài tập khác để cải thiện kỹ năng toán học của mình nhé!