Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
Hình chóp là một trong những khái niệm quan trọng trong hình học, thường xuất hiện trong các bài học Toán học cấp trung học và đại học. Diện tích xung quanh của hình chóp không chỉ có ý nghĩa lý thuyết mà còn có ứng dụng thực tiễn trong nhiều lĩnh vực khác nhau như kiến trúc, thiết kế và sản xuất. Bài viết này sẽ giải thích khái niệm hình chóp, đưa ra công thức tính diện tích xung quanh, cũng như cung cấp một số bài tập từ cơ bản đến nâng cao kèm theo lời giải.
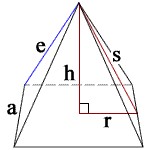
Hình chóp là một khối đa diện có một đáy là một đa giác và các mặt bên là các tam giác. Đỉnh của hình chóp là điểm cách đều các đỉnh của đáy, và hình chiếu của đỉnh xuống mặt phẳng chứa đáy gọi là tâm đáy.
Có nhiều loại hình chóp khác nhau, chẳng hạn như chóp tứ giác, chóp ngũ giác, hay chóp đa giác. Trong hình học, chúng ta thường làm việc với hình chóp đều hoặc không đều, nơi tất cả các cạnh và góc của đáy có thể khác nhau.
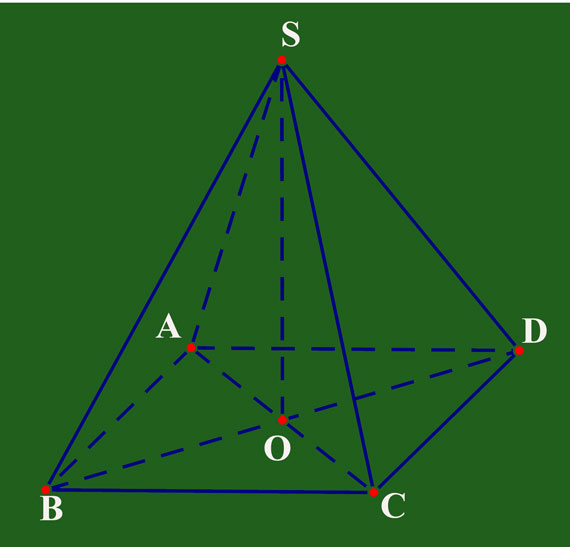
Diện tích xung quanh của hình chóp được tính bằng tổng diện tích của tất cả các mặt bên của hình chóp. Công thức tính diện tích xung quanh hình chóp cụ thể là:
Nếu đáy hình chóp là một đa giác với n cạnh, chiều cao từ đỉnh chóp xuống đáy là h, và chiều dài cạnh đáy là a, diện tích xung quanh (S) được tính bằng công thức:
S = \frac{1}{2} \cdot P \cdot lTrong đó:
– P là chu vi của đáy hình chóp.
– l là chiều cao của các mặt bên (độ dài từ đỉnh hình chóp xuống cạnh đáy).
Trong trường hợp hình chóp có đáy là hình vuông với cạnh dài a, công thức trở thành:
S = 2a \cdot lĐể tính toán diện tích xung quanh của một hình chóp, chúng ta thực hiện theo các bước sau:
1. Xác định hình dạng của đáy: Biết đáy là hình gì (tam giác, tứ giác, ngũ giác,…).
2. Tính chu vi của đáy: Sử dụng công thức chu vi cho hình dạng đáy: (P = \text{tổng chiều dài các cạnh}).
3. Tìm chiều cao của các mặt bên: Đo chiều cao của các mặt bên từ đỉnh hình chóp xuống cạnh đáy.
4. Áp dụng công thức tính diện tích xung quanh: Thay giá trị (P) và (l) vào công thức để tính (S).
Bài tập 1: Diện tích xung quanh hình chóp có đáy là tam giác
Một hình chóp có đáy là tam giác đều với mỗi cạnh dài 6 cm, chiều cao của các mặt bên là 8 cm. Tính diện tích xung quanh của hình chóp.
Giải:
1. Tính chu vi đáy:
– P = 3 \times 6 = 18 cm.
2. Áp dụng công thức:
– S = \frac{1}{2} \times P \times l = \frac{1}{2} \times 18 \times 8 = 72 cm².
Bài tập 2: Diện tích xung quanh hình chóp tứ giác
Hình chóp có đáy là hình vuông với cạnh dài 5 cm, và chiều cao của các mặt bên là 10 cm. Tính diện tích xung quanh.
Giải:
1. Tính chu vi đáy:
– P = 4 \times 5 = 20 cm.
2. Áp dụng công thức:
– S = \frac{1}{2} \times 20 \times 10 = 100 cm².
Bài tập 3: Bài tập nâng cao
Hình chóp có đáy là ngũ giác đều với mỗi cạnh dài 4 cm và chiều cao của các mặt bên là 7 cm. Tính diện tích xung quanh của hình chóp.
Giải:
1. Tính chu vi đáy:
– P = 5 \times 4 = 20 cm.
2. Áp dụng công thức:
– S = \frac{1}{2} \times 20 \times 7 = 70 cm².
Diện tích xung quanh của hình chóp là một trong những khái niệm cơ bản và quan trọng trong hình học. Việc hiểu rõ cách tính diện tích xung quanh không chỉ giúp ích trong các bài tập toán học mà còn có ứng dụng thực tế trong nhiều lĩnh vực. Hy vọng rằng bài viết này đã giúp bạn có cái nhìn tổng quan về hình chóp và diện tích xung quanh của nó. Nếu bạn có bất kỳ câu hỏi nào hoặc cần thêm thông tin, hãy để lại trong phần bình luận dưới đây!