Tính Diện Tích Hình Cầu Online – Công Thức Chuẩn

Hình cầu là một trong những hình dạng cơ bản và quan trọng trong hình học. Trong bài viết này, chúng ta sẽ cùng khám phá diện tích hình cầu, tìm hiểu định nghĩa, công thức tính, và cùng thực hành một số bài tập từ cơ bản đến nâng cao.

Định Nghĩa Hình Cầu

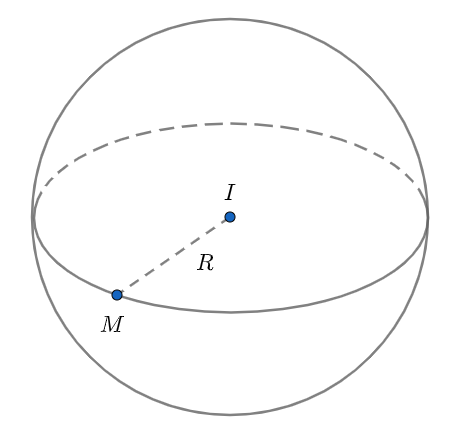
Hình cầu là tập hợp tất cả các điểm trong không gian mà khoảng cách từ một điểm cố định (được gọi là tâm) là một hằng số nhất định, được gọi là bán kính. Một hình cầu có thể được tưởng tượng như là bề mặt của một quả bóng tròn.

Các Thành Phần của Hình Cầu

– Tâm (O): Là điểm nằm ở giữa hình cầu.
– Bán kính (r): Là khoảng cách từ tâm O đến bất kỳ điểm nào trên bề mặt của hình cầu.
– Bề mặt hình cầu: Là tập hợp tất cả các điểm mà cách tâm O một khoảng cách bằng r.

Công Thức Tính Diện Tích Hình Cầu

Diện tích bề mặt của hình cầu được tính bằng công thức sau:

S = 4 \pi r^2

Trong đó:
– S là diện tích bề mặt hình cầu.
– \pi là một hằng số xấp xỉ bằng 3.14159.
– r là bán kính hình cầu.

Giải Thích Công Thức

Công thức này cho thấy rằng diện tích bề mặt của hình cầu tỉ lệ với bình phương bán kính. Có nghĩa là nếu bán kính tăng lên gấp đôi, diện tích bề mặt sẽ tăng lên gấp 4 lần.

Bài Tập Về Diện Tích Hình Cầu

Để nắm vững kiến thức về diện tích hình cầu, chúng ta hãy cùng thực hiện một số bài tập từ cơ bản đến nâng cao.

Bài Tập Cơ Bản

Bài Tập 1: Tính diện tích bề mặt của một hình cầu có bán kính 3 cm.

Giải:
Sử dụng công thức:
S = 4 \pi r^2
thay r = 3 cm vào công thức:
S = 4 \pi \cdot 3^2 = 4 \pi \cdot 9 = 36\pi \approx 113.1 \text{ cm}^2

Bài Tập 2: Một bóng đèn hình cầu có bán kính 5 cm. Tính diện tích bề mặt của bóng đèn.

Giải:
Áp dụng công thức:
S = 4 \pi \cdot 5^2 = 4 \pi \cdot 25 = 100\pi \approx 314.16 \text{ cm}^2

Bài Tập Nâng Cao

Bài Tập 3: Nếu diện tích bề mặt của một hình cầu là 200 cm², hãy tính bán kính của hình cầu đó.

Giải:
Chúng ta có:

S = 4 \pi r^2 = 200

Chia cả hai vế cho 4\pi :

r^2 = \frac{200}{4\pi} = \frac{50}{\pi}

Lấy căn bậc hai hai vế:
r = \sqrt{\frac{50}{\pi}} \approx 3.99 \text{ cm}

Bài Tập 4: Một hình cầu có bán kính tăng từ 2 cm lên 4 cm. Hãy tính sự thay đổi về diện tích bề mặt của hình cầu.

Giải:
– Diện tích trước khi tăng bán kính:
S_1 = 4 \pi \cdot 2^2 = 16\pi \approx 50.27 \text{ cm}^2

– Diện tích sau khi tăng bán kính:
S_2 = 4 \pi \cdot 4^2 = 64\pi \approx 201.06 \text{ cm}^2

– Sự thay đổi diện tích:
\Delta S = S_2 - S_1 = 64\pi - 16\pi = 48\pi \approx 150.79 \text{ cm}^2

Kết Luận

Diện tích mà hình cầu mang lại là một phần quan trọng trong hình học không gian. Qua bài viết này, bạn đã biết được định nghĩa, công thức tính diện tích bề mặt hình cầu, và thực hành một số bài tập từ cơ bản đến nâng cao. Hy vọng rằng kiến thức này sẽ hữu ích cho bạn trong việc học tập và ứng dụng vào thực tế. Hãy luyện tập thêm để nắm vững kiến thức này nhé!