Tính Diện Tích Hình Quạt Online – Công Thức Chuẩn

Hình quạt là một trong những hình dạng phổ biến trong hình học. Nó thường xuất hiện trong thực tế và có nhiều ứng dụng trong thiết kế, kiến trúc cũng như trong những bài toán hình học. Trong bài viết này, chúng ta sẽ tìm hiểu về diện tích của hình quạt, định nghĩa, công thức tính và một vài bài tập từ cơ bản đến nâng cao.

Định Nghĩa Hình Quạt

Hình quạt là phần của mặt phẳng được giới hạn bởi hai bán kính và một cung tròn. Để hình dung dễ hơn, bạn có thể tưởng tượng hình dạng của một chiếc quạt tay hoặc cánh quạt của một chiếc máy bay. Hình quạt có thể được mô tả bởi ba thông số chính: bán kính (R), góc của phần quạt (được tính bằng độ hoặc radian) và diện tích mà nó chiếm.

Công Thức Tính Diện Tích Hình Quạt

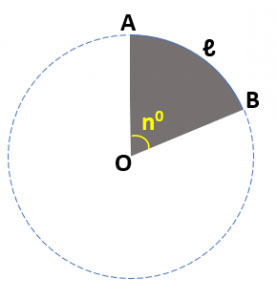
Để tính diện tích của hình quạt, chúng ta có thể sử dụng công thức rất đơn giản. Giả sử bạn có một hình quạt có bán kính là R và góc của hình quạt là θ (tính bằng radian), công thức tính diện tích hình quạt (A) sẽ là:

S = \frac{1}{2} R^2 \theta

Nếu góc θ được cho bằng độ, bạn cần chuyển đổi nó sang radian bởi công thức:

\theta = \frac{\pi}{180} \times \text{độ}

Do đó, công thức tính diện tích hình quạt nếu θ được cho bằng độ sẽ là:

S = \frac{1}{2} R^2 \left( \frac{\pi}{180} \times \text{độ} \right)

Ví Dụ Tính Diện Tích Hình Quạt

Ví Dụ 1: Hình Quạt Cơ Bản

Giả sử bạn có một hình quạt có bán kính R = 5 cm và góc θ = 60 độ. Để tính diện tích của hình quạt, trước tiên chúng ta sẽ chuyển đổi góc này sang radian:

\theta = \frac{\pi}{180} \times 60 = \frac{\pi}{3} \text{ radian}

Tiếp theo, chúng ta sẽ sử dụng công thức tính diện tích:

S = \frac{1}{2} R^2 \theta = \frac{1}{2} \times 5^2 \times \frac{\pi}{3} = \frac{25\pi}{6} \approx 13.09 \text{ cm}^2

Ví Dụ 2: Hình Quạt với Góc Lớn

Bây giờ, hãy xem xét một hình quạt có bán kính R = 10 cm và góc θ = 120 độ. Trước tiên, chúng ta chuyển đổi góc θ sang radian:

\theta = \frac{\pi}{180} \times 120 = \frac{2\pi}{3} \text{ radian}

Sau đó, áp dụng công thức tính diện tích:

S = \frac{1}{2} R^2 \theta = \frac{1}{2} \times 10^2 \times \frac{2\pi}{3} = \frac{100\pi}{3} \approx 104.72 \text{ cm}^2

Các Bài Tập Từ Cơ Bản Đến Nâng Cao

Bài Tập 1: Tính Diện Tích Hình Quạt

Một hình quạt có bán kính 7 cm và góc mở 90 độ. Tính diện tích của hình quạt này.

Bài Tập 2: Hình Quạt Với Bán Kính Khác Nhau

Tính diện tích của một hình quạt có bán kính 3 m và góc θ = 150 độ.

Bài Tập 3: Bài Tập Nâng Cao

Cho một hình quạt có bán kính 8 cm và diện tích là 32π cm². Tính góc θ của hình quạt này.

Gợi Ý Giải

Sử dụng công thức diện tích và thay S = 32π vào:

S = \frac{1}{2} R^2 \theta

Giải phương trình để tìm θ.

Kết Luận

Diện tích hình quạt là một khái niệm đơn giản nhưng có ứng dụng rất rộng rãi trong toán học và thực tế. Bằng việc nắm vững công thức tính và thực hành với các bài tập, bạn sẽ có thể làm chủ được kiến thức về hình quạt. Mong rằng bài viết này đã giúp bạn hiểu rõ hơn về diện tích hình quạt cùng với các công thức và bài tập thực hành thiết thực. Hãy thực hành thường xuyên để củng cố kiến thức nhé!