Tính Thể Tích Hình Trụ Tròn Online Dễ dàng, Công Thức Chuẩn

Trong toán học, hình trụ tròn là một hình khối rất phổ biến, đặc biệt trong các lĩnh vực như kỹ thuật, kiến trúc, và nhiều ngành khoa học khác. Bài viết này sẽ cung cấp cho bạn một cái nhìn tổng quan về thể tích hình trụ tròn, bao gồm định nghĩa, công thức tính, và một vài bài tập từ cơ bản đến nâng cao.

Định Nghĩa Hình Trụ Tròn

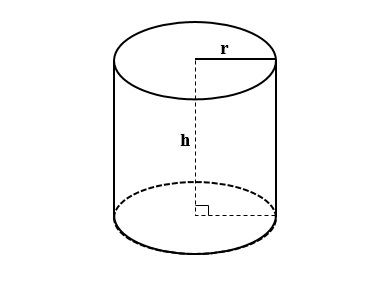
Hình trụ tròn là một hình khối mà mọi điểm trên mặt đáy đều có khoảng cách đến một điểm cố định (tâm đáy) là bằng nhau. Hình trụ tròn bao gồm hai mặt đáy hình tròn và bề mặt phẳng nối giữa chúng.

Các thành phần của hình trụ tròn:
– Bán kính (r): khoảng cách từ tâm đến cạnh của mặt đáy.
– Chiều cao (h): khoảng cách giữa hai mặt đáy.

Công Thức Tính Thể Tích Hình Trụ Tròn

Thể tích V của hình trụ tròn được tính bằng công thức:

V = \pi r^2 h

Trong đó:
– V : thể tích của hình trụ.
– \pi : số pi (khoảng 3.14).
– r : bán kính của đáy hình trụ.
– h : chiều cao của hình trụ.

Ví Dụ Tính Thể Tích Hình Trụ Tròn

Để hiểu sâu hơn về cách tính thể tích hình trụ tròn, chúng ta sẽ giải quyết một số bài tập từ cơ bản đến nâng cao.

Bài Tập 1: Tính Thể Tích Hình Trụ Tròn Cơ Bản

Đề Bài:
Một hình trụ tròn có bán kính đáy là 3 cm và chiều cao là 5 cm. Tính thể tích của hình trụ này.

Giải:
Áp dụng công thức:

V = \pi r^2 h

Thay vào các giá trị:

– r = 3 cm
– h = 5 cm

Ta có:

V = \pi (3)^2 (5) = \pi \cdot 9 \cdot 5 = 45\pi

Khoảng 141,37 cm³ (lấy \pi \approx 3.14 ).

Bài Tập 2: Thay Đổi Chiều Cao

Đề Bài:
Một hình trụ tròn có bán kính đáy là 4 cm và chiều cao là 10 cm. Tính thể tích của hình trụ này.

Giải:
Áp dụng công thức:

V = \pi r^2 h

Thay các giá trị:

– r = 4 cm
– h = 10 cm

Ta có:

V = \pi \cdot 4^2 \cdot 10 = \pi \cdot 16 \cdot 10 = 160\pi

Khoảng 502,65 cm³.

Bài Tập 3: Bài Tập Nâng Cao

Đề Bài:
Một hình trụ có chiều cao gấp đôi bán kính và bán kính bằng 5 cm. Tính thể tích của hình trụ này.

Giải:
Ta có bán kính r = 5 cm, chiều cao h sẽ bằng 2r = 2 \cdot 5 = 10 cm. Áp dụng công thức:

V = \pi r^2 h

Thay vào các giá trị:

V = \pi \cdot 5^2 \cdot 10 = \pi \cdot 25 \cdot 10 = 250\pi

Khoảng 785,4 cm³.

Một Vài Lưu Ý Khi Tính Toán

– Hãy luôn kiểm tra các đơn vị đo vì chiều cao và bán kính cần phải đồng nhất (cm, m, km…).
– Giữ chính xác trong phép tính, đặc biệt là khi sử dụng số pi, có thể sử dụng giá trị gần đúng 3.14 hoặc giá trị chính xác hơn là \frac{22}{7} .

Kết Luận

Hình trụ tròn là một trong những hình khối có ứng dụng rộng rãi và việc hiểu rõ cách tính thể tích của nó rất quan trọng. Bạn có thể áp dụng các công thức trên để giải quyết nhiều bài tập liên quan đến hình trụ tròn trong thực tiễn. Hy vọng bài viết này sẽ giúp bạn có thêm kiến thức và kỹ năng trong việc tính toán thể tích hình trụ tròn. Nếu bạn có thêm câu hỏi hoặc bài tập nào cần giải quyết, hãy để lại câu hỏi của bạn trong phần bình luận nhé!