Tính Thể Tích Hình Cầu Online Nhanh Chóng, Dễ dàng, Công Thức Chuẩn

Hình cầu là một trong những hình khối đặc trưng trong hình học không gian, và việc hiểu cách tính thể tích của nó là một phần quan trọng trong việc học toán. Bài viết này sẽ giúp bạn nắm rõ định nghĩa thể tích hình cầu, công thức tính thể tích, cũng như cung cấp một số bài tập từ cơ bản đến nâng cao để bạn có thể luyện tập.

Định Nghĩa Hình Cầu

Hình cầu là tập hợp tất cả những điểm trong không gian với khoảng cách không đổi (được gọi là bán kính) đến một điểm cố định (được gọi là tâm hình cầu). Ký hiệu bán kính là r và tâm hình cầu được ký hiệu là O .

Công Thức Tính Thể Tích Hình Cầu

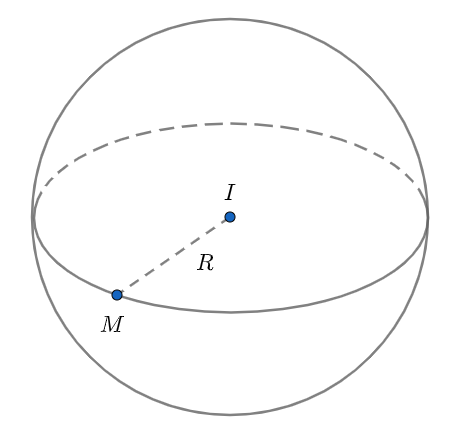
Thể tích của hình cầu được tính theo công thức:

V = \frac{4}{3} \pi r^3

Trong đó:
– V là thể tích của hình cầu.
– r là bán kính của hình cầu.
– \pi là số Pi, xấp xỉ bằng 3.14.

Cách Tính Thể Tích Hình Cầu

Bước 1: Xác định Bán Kính

Để tính thể tích của hình cầu, điều đầu tiên là xác định bán kính r . Nếu bạn có đường kính d , bạn có thể tính bán kính bằng công thức:

r = \frac{d}{2}

Bước 2: Áp Dụng Công Thức

Sau khi đã biết bán kính, bạn chỉ cần thay giá trị vào công thức tính thể tích.

Bài Tập Cơ Bản

Bài Tập 1: Cho một hình cầu có bán kính r = 3 cm. Tính thể tích của hình cầu đó.**

Giải:

Áp dụng công thức:

V = \frac{4}{3} \pi \cdot 3^3 = \frac{4}{3} \pi \cdot 27 = 36 \pi \approx 113.1 \text{ cm}^3

Bài Tập 2: Hình cầu có đường kính d = 10 cm. Tính thể tích của hình cầu này.

Giải:

Trước tiên, tính bán kính:

r = \frac{10}{2} = 5 \text{ cm}

Tiếp theo, áp dụng công thức tính thể tích:

V = \frac{4}{3} \pi \cdot 5^3 = \frac{4}{3} \pi \cdot 125 = \frac{500}{3} \pi \approx 523.6 \text{ cm}^3

Bài Tập Nâng Cao

Bài Tập 3: Cho một hình cầu có thể tích là 288 \pi cm³. Tính bán kính của hình cầu.

Giải:

Chúng ta có thể sử dụng công thức thể tích để tính bán kính:

V = \frac{4}{3} \pi r^3

Thay V vào công thức:

288 \pi = \frac{4}{3} \pi r^3

Chia hai bên cho \pi :

288 = \frac{4}{3} r^3

Nhân hai bên với \frac{3}{4} :

r^3 = 288 \cdot \frac{3}{4} = 216

Lấy căn bậc ba của cả hai bên:

r = \sqrt[3]{216} = 6 \text{ cm}

Bài Tập 4: Tính thể tích của hình cầu có bán kính tăng thêm 2 cm so với hình cầu có bán kính 4 cm.

Giải:

Hình cầu đầu tiên có bán kính 4 cm:

V_1 = \frac{4}{3} \pi \cdot 4^3 = \frac{4}{3} \pi \cdot 64 = \frac{256}{3} \pi \approx 268.1 \text{ cm}^3

Hình cầu thứ hai có bán kính 4 + 2 = 6 cm:

V_2 = \frac{4}{3} \pi \cdot 6^3 = \frac{4}{3} \pi \cdot 216 = 288 \pi \approx 904.3 \text{ cm}^3

Kết Luận

Như vậy, bài viết đã giúp bạn hiểu rõ về thể tích hình cầu, từ định nghĩa, công thức tính đến các bài tập từ cơ bản đến nâng cao. Việc nắm chắc công thức và thực hành giải bài tập sẽ giúp bạn thành thạo hơn trong việc áp dụng kiến thức hình học này vào các bài toán thực tế. Hy vọng rằng bạn sẽ áp dụng kiến thức đã học để giải quyết các bài toán liên quan đến thể tích hình cầu!