Tính Chu Vi Hình Thoi Online Dễ Dàng – Công Thức Chuẩn

Hình thoi (hay còn gọi là tứ giác đều) là một trong những hình học cơ bản mà chúng ta thường gặp trong toán học. Nó không chỉ là một hình có ít thuộc tính thú vị mà còn là một khái niệm quan trọng trong nhiều lĩnh vực như kiến trúc, thiết kế hình học và thậm chí trong các ứng dụng khoa học. Trong bài viết này, chúng ta sẽ tìm hiểu về chu vi hình thoi, định nghĩa, công thức tính chu vi và các bài tập từ cơ bản đến nâng cao.

Tính Chu Vi Hình Thoi

Nhập độ dài cạnh a: Chọn đơn vị: m cm mm mile yard feet inch Tính chu vi

Định Nghĩa Hình Thoi

Hình thoi là một loại tứ giác có tất cả bốn cạnh đều bằng nhau. Các góc của hình thoi không nhất thiết phải bằng nhau, nhưng tổng các góc nội tiếp của hình thoi vẫn phải bằng 360 độ. Hình thoi có đặc điểm nổi bật là hai đường chéo của nó cắt nhau tại một điểm và chia nhau thành hai đoạn bằng nhau. Đường chéo của hình thoi cũng có tính chất là vuông góc với nhau.

Công Thức Tính Chu Vi Hình Thoi

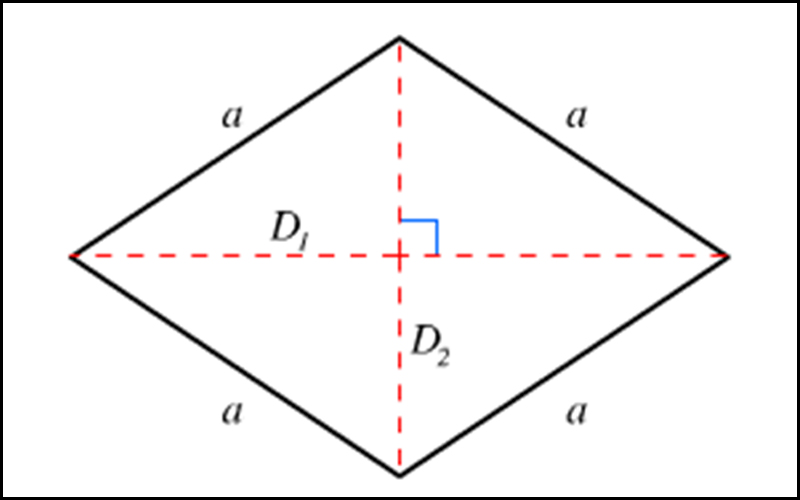
Để tính chu vi của hình thoi, ta cần biết độ dài của một cạnh. Công thức tính chu vi của hình thoi được biểu diễn như sau:

Trong đó:
– P là chu vi của hình thoi.
– a là độ dài của một cạnh.

Ví Dụ Tính Chu Vi Hình Thoi

1. Bài Tập Cơ Bản: Một hình thoi có độ dài cạnh là 5 cm. Tính chu vi của hình thoi.
– Giải: Áp dụng công thức trên
P = 4 \times 5 = 20 \text{ cm}

2. Bài Tập Nâng Cao: Một hình thoi có chu vi là 40 cm. Tính độ dài mỗi cạnh của hình thoi.
– Giải: Sử dụng công thức chu vi
40 = 4a \implies a = \frac{40}{4} = 10 \text{ cm}

Các Tính Chất Của Hình Thoi

Ngoài việc tính chu vi, hình thoi còn có nhiều tính chất thú vị khác:

1. Độ dài các đường chéo: Hai đường chéo của hình thoi không những vuông góc mà còn chia nhau thành các đoạn bằng nhau.
2. Diện tích: Diện tích của hình thoi tính theo công thức:
S = \frac{1}{2} \times d_1 \times d_2
Trong đó d_1 và d_2 là độ dài hai đường chéo.
3. Góc: Các góc đối diện của hình thoi bằng nhau và tổng của hai góc kề nhau là 180 độ.

Bài Tập Tính Diện Tích Hình Thoi

1. Bài Tập Cơ Bản: Tính diện tích của một hình thoi có hai đường chéo lần lượt là 6 cm và 8 cm.
– Giải:
S = \frac{1}{2} \times 6 \times 8 = 24 \text{ cm}^2

2. Bài Tập Nâng Cao: Một hình thoi có diện tích là 30 cm² và một đường chéo dài 10 cm. Tính độ dài đường chéo còn lại.
– Giải:
30 = \frac{1}{2} \times 10 \times d_2 \implies d_2 = \frac{30 \times 2}{10} = 6 \text{ cm}

Kết Luận

Hình thoi là một trong những hình dạng cơ bản nhất trong hình học, với các tính chất độc đáo và ứng dụng rộng rãi. Hi vọng bài viết này đã giúp bạn hiểu rõ hơn về định nghĩa cũng như công thức tính chu vi và diện tích của hình thoi. Những bài tập từ cơ bản đến nâng cao sẽ giúp bạn củng cố kiến thức và kỹ năng giải toán của bản thân. Nếu bạn có bất kỳ câu hỏi nào về hình thoi hoặc các chủ đề khác trong hình học, hãy để lại trong phần bình luận dưới đây!