Tính Chu Vi Hình Bình Hành Online Dễ Dàng – Công Thức Chuẩn

Hình bình hành là một trong những hình học cơ bản được sử dụng thường xuyên trong nhiều lĩnh vực như toán học, kiến trúc hay kỹ thuật. Việc tính toán chu vi hình bình hành là một phần quan trọng trong việc học và áp dụng hình học. Trong bài viết này, chúng ta sẽ cùng nhau tìm hiểu định nghĩa, công thức tính chu vi hình bình hành, cũng như làm một vài bài tập từ cơ bản đến nâng cao để củng cố kiến thức.

Định Nghĩa Hình Bình Hành

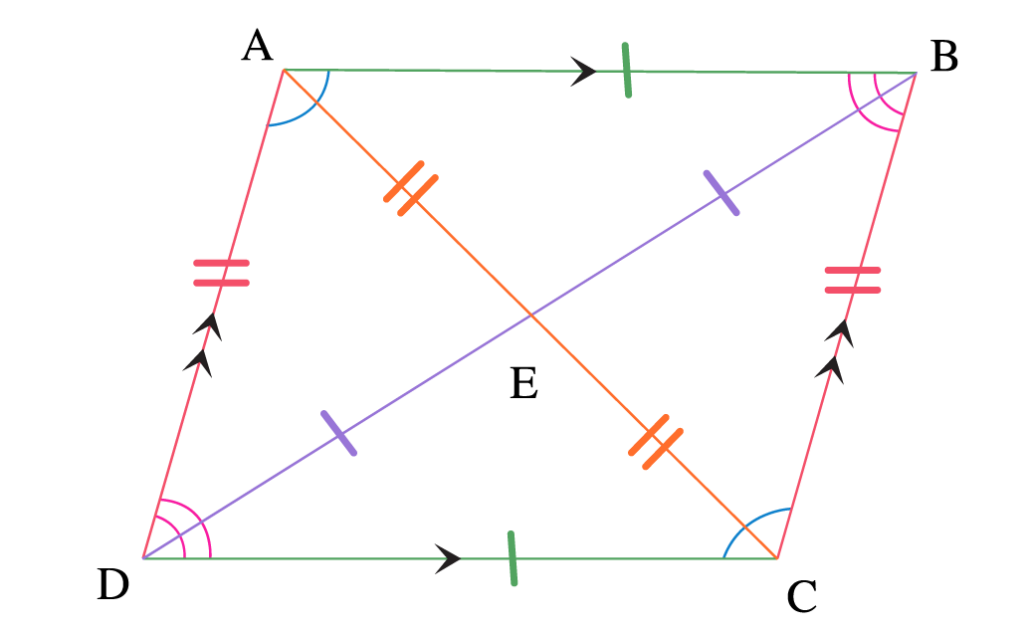
Hình bình hành là một hình tứ giác có hai cặp cạnh đối song song và bằng nhau. Các góc đối của hình bình hành cũng bằng nhau. Hình hình bình hành có thể bao gồm các hình đặc biệt khác như hình chữ nhật, hình thoi.

Trong hình bình hành, nếu gọi hai cạnh liền kề là a và b, và góc giữa chúng là α, thì hình bình hành có những đặc điểm sau:

– Các cạnh đối đều bằng nhau: AB = CD và AD = BC.
– Các góc đối bằng nhau: ∠A = ∠C và ∠B = ∠D.
– Tổng các góc trong hình bình hành luôn bằng 360 độ.

Công Thức Tính Chu Vi Hình Bình Hành

Chu vi của hình bình hành được tính bằng tổng độ dài của tất cả các cạnh của nó. Công thức tính chu vi hình bình hành được biểu thị như sau:

P = 2(a + b)

Trong đó:
– P là chu vi của hình bình hành.
– a là độ dài một cạnh của hình bình hành.
– b là độ dài cạnh còn lại của hình bình hành.

Cách tính này rất đơn giản, bạn chỉ cần biết độ dài hai cạnh bên cạnh nhau của hình bình hành là có thể tính được chu vi.

Các Bài Tập Tính Chu Vi Hình Bình Hành

Bài Tập 1: Tính Chu Vi Hình Bình Hành Cơ Bản

Giả sử bạn có một hình bình hành với độ dài cạnh a = 5cm và b = 3cm. Tính chu vi P của hình bình hành này.

Giải:

Áp dụng công thức tính chu vi:

P = 2(a + b) = 2(5 + 3) = 2 \times 8 = 16 \text{ cm}

Vậy chu vi của hình bình hành là 16 cm.

Bài Tập 2: Hình Bình Hành Với Thông Tin Thêm

Một hình bình hành có một cạnh dài 10m, và độ dài cạnh còn lại là 6m. Hãy tính chu vi của hình bình hành này.

Giải:

Sử dụng công thức:

P = 2(a + b) = 2(10 + 6) = 2 \times 16 = 32 \text{ m}

Nên chu vi của hình bình hành là 32 m.

Bài Tập 3: Bài Tập Nâng Cao

Một hình bình hành có chu vi là 50m và độ dài một cạnh là 18m. Tính chiều dài cạnh còn lại.

Giải:

Chúng ta có công thức chu vi:

P = 2(a + b)

Thay P = 50m và a = 18m vào phương trình:

50 = 2(18 + b)

Chia cả hai bên cho 2:

25 = 18 + b

Giải phương trình để tìm b:

b = 25 - 18 = 7 \text{ m}

Vậy chiều dài cạnh còn lại là 7 m.

Bài Tập 4: Bài Tập Thực Tế

Một khu vườn hình bình hành có các cạnh dài 15m và 25m. Chủ sở hữu muốn rào lại vườn. Hỏi tổng chiều dài hàng rào cần thiết là bao nhiêu?

Giải:

Dựa trên công thức:

P = 2(a + b) = 2(15 + 25) = 2 \times 40 = 80 \text{ m}

Do đó, chiều dài hàng rào cần thiết là 80 m.

Kết Luận

Trong bài viết này, chúng ta đã tìm hiểu về định nghĩa, công thức tính chu vi hình bình hành và giải quyết một số bài tập từ cơ bản đến nâng cao. Hình bình hành không chỉ là một khái niệm lý thuyết mà còn ứng dụng thực tế trong nhiều lĩnh vực. Việc hiểu rõ cách tính chu vi sẽ giúp bạn ứng dụng hình học một cách hiệu quả hơn trong cuộc sống hàng ngày.

Nếu bạn còn bất kỳ thắc mắc nào liên quan đến hình bình hành hay chu vi của nó, hãy tham gia vào cộng đồng học tập và chia sẻ kinh nghiệm của bạn nhé!