Tính Diện Tích Hình Thang Online Chính Xác, Chia sẻ Công Thức Chuẩn

Hình thang là một trong những hình dạng cơ bản trong hình học, được biết đến rộng rãi trong các bài toán liên quan đến diện tích. Bài viết này sẽ chia sẻ về diện tích hình thang, định nghĩa, công thức tính và thực hành qua một số bài tập từ cơ bản đến nâng cao.

Định Nghĩa Hình Thang

Hình thang là một tứ giác (hình có 4 cạnh) có hai cạnh song song gọi là hai đáy và hai cạnh còn lại không song song. Hai cạnh song song này được gọi là đáy của hình thang, trong khi hai cạnh không song song được gọi là cạnh bên.

Các Loại Hình Thang Đặc Biệt

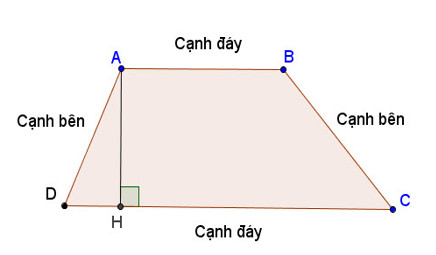
Có hai loại hình thang đặc biệt:

• Hình thang cân: Là hình thang mà hai cạnh bên có độ dài bằng nhau.
• Hình thang vuông: Là hình thang có một trong hai cạnh bên vuông góc với hai đáy.

Công Thức Tính Diện Tích Hình Thang

Công thức tính diện tích S của hình thang được đưa ra như sau:

S = \frac{(a + b) \cdot h}{2}

Trong đó:
– a : Độ dài đáy thứ nhất.
– b : Độ dài đáy thứ hai.
– h : Chiều cao của hình thang, là khoảng cách giữa hai đáy.

Giải Thích Công Thức

Công thức tính diện tích hình thang tương tự như cách tính diện tích hình chữ nhật, tuy nhiên nó được điều chỉnh để phù hợp với hình dạng của hình thang. Bằng cách cộng lại độ dài hai đáy và nhân với chiều cao, chúng ta có được tổng diện tích của hình thang.

Một Số Bài Tập Thực Hành

Bài Tập 1: Tính Diện Tích Hình Thang Cơ Bản

Cho một hình thang với đáy trên dài 5 cm, đáy dưới dài 9 cm và chiều cao 4 cm. Tính diện tích của hình thang.

Giải

Áp dụng công thức:

S = \frac{(5 + 9) \cdot 4}{2} = \frac{14 \cdot 4}{2} = \frac{56}{2} = 28 \text{ cm}^2

Vậy diện tích của hình thang là 28 cm².

Bài Tập 2: Hình Thang Với Đáy Khác Nhau

Cho một hình thang có đáy trên dài 7 cm, đáy dưới dài 10 cm và chiều cao 6 cm. Tính diện tích của hình thang.

Giải

Áp dụng công thức:

S = \frac{(7 + 10) \cdot 6}{2} = \frac{17 \cdot 6}{2} = \frac{102}{2} = 51 \text{ cm}^2

Vậy diện tích của hình thang là 51 cm².

Bài Tập 3: Tìm Chiều Cao Khi Biết Diện Tích

Cho một hình thang có đáy trên dài 8 cm, đáy dưới dài 12 cm, và diện tích là 80 cm². Tính chiều cao của hình thang.

Giải

Ta biết diện tích và muốn tìm chiều cao h , áp dụng công thức:

S = \frac{(a + b) \cdot h}{2} => h = \frac{2S}{a + b}

Thay các giá trị vào:

h = \frac{2 \cdot 80}{8 + 12} = \frac{160}{20} = 8 \text{ cm}

Vậy chiều cao của hình thang là 8 cm.

Bài Tập 4: Bài Toán Nâng Cao

Một hình thang vuông có đáy dài 10 cm, đáy ngắn dài 6 cm. Tính diện tích và chiều cao của hình thang nếu bạn biết rằng diện tích của nó là 40 cm².

Giải

Ta biết đáy và diện tích, áp dụng công thức tính chiều cao:

S = \frac{(a + b) \cdot h}{2} => h = \frac{2S}{a + b}

Thay các giá trị vào:

h = \frac{2 \cdot 40}{10 + 6} = \frac{80}{16} = 5 \text{ cm}

Và diện tích cũng được xác nhận là:

S = \frac{(10 + 6) \cdot 5}{2} = \frac{16 \cdot 5}{2} = 40 \text{ cm}^2

Bài Tập 5: Tìm Đáy Khi Biết Diện Tích

Cho một hình thang có diện tích 72 cm², đáy trên dài 8 cm, và chiều cao là 6 cm. Tìm đáy dưới.

Giải

Chúng ta sẽ sử dụng công thức tính diện tích và thay thế:

S = \frac{(a + b) \cdot h}{2}

Nên ta có:

72 = \frac{(8 + b) \cdot 6}{2}

Giải phương trình:

144 = (8 + b) \cdot 6 24 = 8 + b => b = 16 \text{ cm}

Vậy đáy dưới dài 16 cm.

Kết Luận

Diện tích hình thang là một khái niệm cơ bản nhưng rất hữu ích trong toán học và nhiều lĩnh vực khác. Qua bài viết, bạn đã được tìm hiểu về định nghĩa, công thức và một số bài tập tính diện tích hình thang từ cơ bản đến nâng cao. Hy vọng rằng những kiến thức này sẽ giúp bạn nắm vững hơn về hình thang và áp dụng một cách hiệu quả trong học tập cũng như trong cuộc sống hàng ngày.