Tính Diện Tích Hình Tròn Online Nhanh Chóng, Chính Xác, Công Thức Chuẩn

Hình tròn là một trong những hình học cơ bản nhất mà chúng ta thường gặp trong cuộc sống hàng ngày. Bài viết sẽ chia sẻ máy tính diện tích hình tròn online chính xác, nhanh chóng, cũng như tìm hiểu chi tiết về định nghĩa, công thức và bài tập tính diện tích hình tròn.

Định Nghĩa Hình Tròn

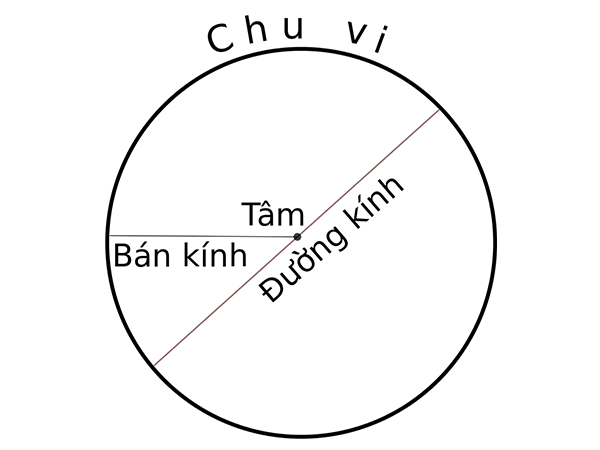
Hình tròn được định nghĩa là tập hợp tất cả các điểm nằm cách đều một điểm cố định (gọi là tâm của hình tròn) một khoảng cách nhất định (được gọi là bán kính). Trong hình học, một số ký hiệu thường thấy là:
– S : diện tích của hình tròn
– r : bán kính của hình tròn
– P : chu vi của hình tròn
– O : tâm của hình tròn

Công Thức Tính Diện Tích Hình Tròn

Để tính diện tích của hình tròn, chúng ta sử dụng công thức:

S = \pi r^2

Trong đó:
– S là diện tích hình tròn
– \pi (pi) là một hằng số, xấp xỉ bằng 3.14 hoặc 22/7, biểu thị cho tỷ lệ giữa chu vi và đường kính của hình tròn.
– r là bán kính của hình tròn.

Ví Dụ Bài Tập Từ Cơ Bản Đến Nâng Cao

Bài Tập Cơ Bản

Bài 1: Tính diện tích của hình tròn có bán kính là 5 cm.

Giải:

Theo công thức, ta có:

S = \pi r^2 = \pi \times 5^2 = \pi \times 25

Nếu lấy \pi xấp xỉ là 3.14, ta tính được:

S\approx 3.14 \times 25 \approx 78.5 \text{ cm}^2

Bài Tập Trung Bình

Bài 2: Một hình tròn có diện tích là 50 cm². Tính bán kính của hình tròn.

Giải:

Sử dụng công thức diện tích, chúng ta có thể tìm ra bán kính:

50 = \pi r^2

Suy ra:

r^2 = \frac{50}{\pi}

Sau đó, tính:

r \approx \sqrt{\frac{50}{3.14}} \approx \sqrt{15.92} \approx 3.98 \text{ cm}

Bài Tập Nâng Cao

Bài 3: Tính diện tích của một hình tròn có đường kính là 10 cm.

Giải:

Trước tiên, bán kính sẽ là nửa của đường kính:

r = \frac{10}{2} = 5 \text{ cm}

Áp dụng vào công thức diện tích:

S = \pi r^2 = \pi \times 5^2 = \pi \times 25 \approx 78.5 \text{ cm}^2

Kết Luận

Tính diện tích hình tròn là một kỹ năng cơ bản mà mỗi người cần nắm vững. Với công thức S = \pi r^2 , bạn có thể dễ dàng tính toán diện tích cho bất kỳ hình tròn nào. Hy vọng qua bài viết này, bạn đã có thêm kiến thức và kỹ năng trong việc làm việc với hình tròn. Hãy thử sức với các bài tập để nâng cao khả năng nhé!