Tính Diện Tích Toàn Phần Hình Chóp Online – Công Thức Chuẩn

Hình chóp là một trong những khối hình học phổ biến trong toán học, đặc biệt trong các bài tập liên quan đến hình học không gian. Trong bài viết này, chúng ta sẽ cùng tìm hiểu về diện tích toàn phần của hình chóp, bao gồm định nghĩa, công thức tính, cũng như một vài bài tập từ cơ bản đến nâng cao.

Định Nghĩa Hình Chóp

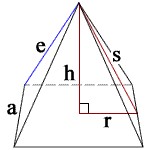
Hình chóp là một khối đa diện có một mặt đáy là một polygon (hình đa giác) và tất cả các đỉnh của mặt đáy đều nối với một điểm gọi là đỉnh chóp. Hình chóp có thể được phân loại thành nhiều loại khác nhau, nhưng trong khuôn khổ bài viết này, chúng ta sẽ chủ yếu tập trung vào hình chóp tam giác và hình chóp tứ giác.

– Hình chóp tam giác: Là hình chóp có đáy là một tam giác.
– Hình chóp tứ giác: Là hình chóp có đáy là một tứ giác (hình vuông, hình chữ nhật, hình thang, …).

Công Thức Tính Diện Tích Toàn Phần Hình Chóp

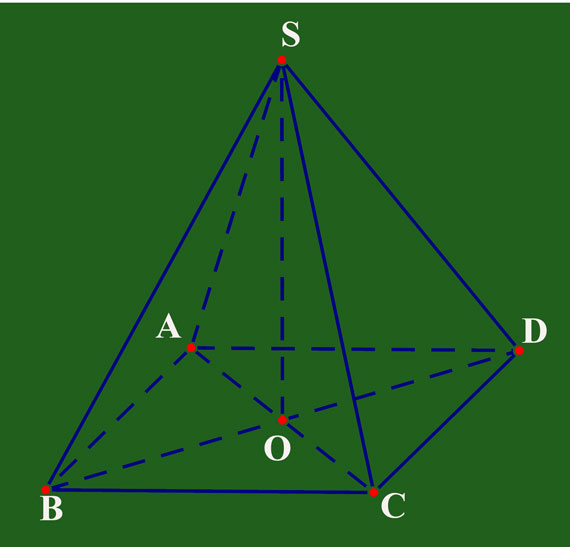
Diện tích toàn phần của hình chóp được tính bằng tổng diện tích mặt đáy và diện tích các mặt bên. Công thức tính cụ thể như sau:

1. Diện tích mặt đáy S_đáy : Tùy thuộc vào loại đáy:
– Nếu đáy là một tam giác thì:
S_{đáy} = \frac{1}{2} \cdot a \cdot h \text{ (với  a là cạnh đáy và h là chiều cao của tam giác)}
– Nếu đáy là một tứ giác thì diện tích sẽ tính theo công thức phổ thông cho tứ giác tương ứng.

2. Diện tích mặt bên S_{bên}:
– Diện tích các mặt bên của hình chóp là tổng diện tích các tam giác tạo nên các mặt bên. Nếu rìa đáy có n cạnh, thì diện tích mặt bên tính như sau:
S_{bên} = S_1 + S_2 + ... + S_n
Trong đó S_i là diện tích của mặt bên i.

3. Diện tích toàn phần S_t :
Cuối cùng, diện tích toàn phần được tính bằng:
S_{t} = S_{đáy} + S_{bên}

Bài Tập Tính Diện Tích Toàn Phần Hình Chóp

Bài Tập Cơ Bản

Bài Tập 1: Tính diện tích toàn phần của một hình chóp tứ giác có đáy là hình vuông với cạnh dài 4 cm và chiều cao của mặt bên là 6 cm.

Giải:

– Diện tích mặt đáy:
S_{đáy} = a^2 = 4^2 = 16 \text{ cm}^2

– Diện tích mặt bên:

Diện tích của mỗi mặt bên là một tam giác có đáy là cạnh của hình vuông (4 cm) và chiều cao là chiều cao mặt bên (6 cm):

S_{1} = S_{2} = S_{3} = S_{4} = \frac{1}{2} \cdot 4 \cdot 6 = 12 \text{ cm}^2

Tổng diện tích mặt bên:

S_{bên} = 4 \cdot 12 = 48 \text{ cm}^2

– Diện tích toàn phần:

S_{t} = S_{đáy} + S_{bên} = 16 + 48 = 64 \text{ cm}^2

Bài Tập Nâng Cao

Bài Tập 2: Tính diện tích toàn phần của một hình chóp có đáy là tam giác đều với cạnh 6 cm và chiều cao của hình chóp là 8 cm. Hình chóp có chiều cao mặt bên vuông góc với mặt đáy.

Giải:

– Diện tích mặt đáy (tam giác đều):
S_{đáy} = \frac{\sqrt{3}}{4} \cdot a^2 = \frac{\sqrt{3}}{4} \cdot 6^2 = 9\sqrt{3} \text{ cm}^2

– Diện tích mặt bên:
Diện tích mỗi mặt bên cũng là một tam giác với đáy là cạnh của đáy hình chóp (6 cm) và chiều cao là chiều cao mặt bên (tính từ đỉnh chóp xuống cạnh đáy):
S_{i} = \frac{1}{2} \cdot 6 \cdot 8 = 24 \text{ cm}^2
Tính diện tích của 3 mặt bên:
S_{bên} = 3 \cdot 24 = 72 \text{ cm}^2

– Diện tích toàn phần:
S_{t} = S_{đáy} + S_{bên} = 9\sqrt{3} + 72 \text{ cm}^2

Kết Luận

Diện tích toàn phần của hình chóp là một phần quan trọng trong hình học không gian, giúp chúng ta hiểu rõ hơn về cấu trúc và diện tích của các khối hình học. Qua các ví dụ và bài tập trên, hy vọng bạn đã nắm vững kiến thức này và có thể áp dụng nó vào các bài toán liên quan. Nếu bạn có bất kỳ thắc mắc nào, đừng ngần ngại để lại câu hỏi trong phần bình luận!