Tính Diện Tích Xung Quanh Hình Nón Cụt Online – Công Thức Chuẩn

Hình nón cụt là một trong những hình khối thú vị trong hình học phẳng. Bài viết này sẽ giúp bạn hiểu rõ hơn về diện tích xung quanh hình nón cụt, cũng như cách tính toán và bài tập áp dụng.

Định Nghĩa Hình Nón Cụt

Hình nón cụt là khối hình được tạo ra từ một hình nón khi cắt nó bằng một mặt phẳng song song với đáy của hình nón. Hình nón cụt có hai đáy: một đáy lớn và một đáy nhỏ, và các đường sinh nối liền giữa hai đáy.

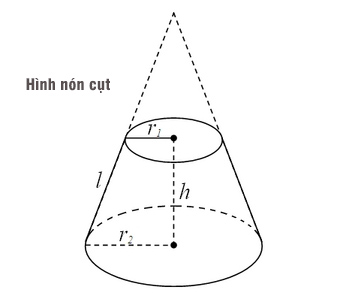
Ví dụ về Hình Nón Cụt

Công Thức Tính Diện Tích Xung Quanh Hình Nón Cụt

Để tính diện tích xung quanh của hình nón cụt, chúng ta cần biết bán kính của hai đáy (r1 và r2) cũng như chiều cao của hình nón cụt (h). Diện tích xung quanh của nó có thể được tính bằng công thức sau:

Công Thức:

Diện tích xung quanh (S) được tính bằng:

S = \pi (r_1 + r_2) l

Trong đó:
– r_1 là bán kính đáy lớn,
– r_2 là bán kính đáy nhỏ,
– l  là độ dài đường sinh của hình nón cụt, được tính bằng công thức:

l = \sqrt{(r_1 - r_2)^2 + h^2}

Giải Thích Công Thức

– Bán Kính Đáy (r1 và r2): Là khoảng cách từ tâm đáy đến vành đáy. Bán kính lớn (r1) nằm ở đáy lớn của hình nón cụt, và bán kính nhỏ (r2) nằm ở đáy nhỏ.
– Chiều Cao (h): Là đoạn thẳng vuông góc từ đáy lớn đến đáy nhỏ.
– Đường Sinh (s): Là độ dài cac tuyến đường từ điểm biên của đáy lớn đến điểm biên của đáy nhỏ.

Bài Tập Về Tính Diện Tích Xung Quanh Hình Nón Cụt

Bài Tập 1: Tính Diện Tích Xung Quanh

Cho một hình nón cụt có bán kính đáy lớn r_1 = 5 cm, bán kính đáy nhỏ r_2 = 3 cm và chiều cao h = 4 cm. Tính diện tích xung quanh của hình nón cụt này.

Giải:

Bước 1: Tính đường sinh l

l = \sqrt{(5 - 3)^2 + 4^2} = \sqrt{2^2 + 4^2} = \sqrt{4 + 16} = \sqrt{20} = 2\sqrt{5}

Bước 2: Áp dụng công thức tính diện tích xung quanh

S = \pi (5 + 3) \cdot 2\sqrt{5} = \pi \cdot 8 \cdot 2\sqrt{5} = 16\pi\sqrt{5} \approx 71.58 \text{ cm}^2

Bài Tập 2: Tính Bán Kính và Chiều Cao

Trong hình nón cụt, nếu diện tích xung quanh là 40π cm² thì hãy tính chiều cao và bán kính nếu bán kính đáy nhỏ là 2 cm.

Giải:

Áp dụng công thức diện tích xung quanh:

40\pi = \pi (r_1 + 2) l

Bước 1: Gọi r1 là bán kính đáy lớn. Ta có:

40 = r_1 + 2 r_1 = 40 - 2 = 38 \text{ cm}

Bước 2: Sử dụng công thức tính đường sinh

l = \sqrt{(r_1 - r_2)^2 + h^2} = \sqrt{(38 - 2)^2 + h^2} = \sqrt{36^2 + h^2} = \sqrt{1296 + h^2}

Bước 3: Lấy vào công thức tính diện tích:

40 = (38 + 2) \sqrt{1296 + h^2} = 40 \sqrt{1296 + h^2}

Kết luận: Từ bài tập trên, bạn có thể thấy rằng diện tích xung quanh của hình nón cụt đóng vai trò quan trọng trong việc tính toán và hiểu biết về hình học.

Kết Luận

Bài viết này đã cung cấp cho bạn những kiến thức cần thiết để tính toán diện tích xung quanh của hình nón cụt, với các công thức và ví dụ minh họa. Từ cơ bản đến nâng cao, việc làm quen với các công thức hình học này sẽ giúp bạn áp dụng chúng trong nhiều lĩnh vực khác nhau. Chúc bạn thành công trong học tập!

Bạn có thể tham khảo thêm tài liệu và thực hành thêm bài tập để củng cố kiến thức của mình về hình nón cụt. Hãy để lại câu hỏi nếu bạn cần trợ giúp thêm nhé!