Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
Tính Diện Tích Xung Quanh Hình Nón Online Dễ Dàng, Công Thức Chuẩn
Hình nón là một trong những hình khối cơ bản trong hình học, rất quen thuộc trong đời sống cũng như trong toán học. Một trong những khái niệm quan trọng liên quan đến hình nón là diện tích xung quanh. Bài viết này sẽ giúp bạn hiểu rõ về định nghĩa, công thức tính diện tích xung quanh hình nón, cũng như một số bài tập từ cơ bản đến nâng cao.
Tính Diện Tích Xung Quanh Hình Nón
Định Nghĩa Hình Nón
Hình nón là một hình khối có đáy là một hình tròn và được tạo ra bởi việc quay một tam giác vuông quanh một cạnh của nó. Các điểm trên bề mặt của hình nón đều nằm gần đáy và có điểm đỉnh cao nhất, thường được gọi là “đỉnh của hình nón”.
Các Thành Phần Của Hình Nón
– Bán Kính (r): Bán kính của đáy hình nón.
– Chiều Cao (h): Đo khoảng cách từ đỉnh của hình nón xuống mặt phẳng đáy.
– Đường Sinh (l): Đo khoảng cách từ đỉnh đến một điểm trên đường tròn đáy. Nó được tính bằng khoảng cách giữa đỉnh và điểm trên đường tròn.
Diện Tích Xung Quanh Hình Nón
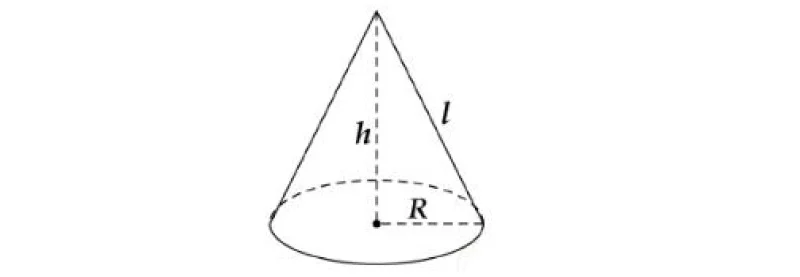
Diện tích xung quanh của hình nón là diện tích của bề mặt bên ngoài mà không tính diện tích đáy. Để tính diện tích xung quanh, chúng ta sử dụng công thức sau:
Công Thức Tính Diện Tích Xung Quanh Hình Nón
Diện tích xung quanh (S) của hình nón được tính bằng công thức:
S = \pi r lTrong đó:
– S là diện tích xung quanh.
– r là bán kính đáy của hình nón.
– l là độ dài của đường sinh.
Cách Tính Độ Dài Đường Sinh
Để tính được diện tích xung quanh, bạn cần biết chiều cao h và bán kính r của đáy. Độ dài tạo thành có thể được tính bằng định lý Pythagoras:
l = \sqrt{r^2 + h^2}Trong đó:
– l là tạo thành,
– r là bán kính,
– h là chiều cao.
Ví Dụ và Bài Tập về tính diện tích xung quanh hình nón
Bài Tập Cơ Bản
Bài Tập 1: Cho một hình nón có bán kính đáy r = 3 cm và chiều cao h = 4 cm. Tính diện tích xung quanh của hình nón.
Giải:
1. Tính đường sinh l :
2. Tính diện tích xung quanh S :
A = \pi \cdot 3 \cdot 5 = 15\pi \text{ cm}^2 \approx 47.12 \text{ cm}^2Bài Tập Nâng Cao
Bài Tập 2:
Một hình nón có chiều cao gấp đôi bán kính đáy. Nếu bán kính đáy là r = 2 cm, tính diện tích xung quanh hình nón.
Giải:
1. Tính chiều cao:
h = 2r = 2 \cdot 2 = 4 \text{ cm}
2. Tính đường sinh l :
l = \sqrt{r^2 + h^2} = \sqrt{2^2 + 4^2} = \sqrt{4 + 16} = \sqrt{20} = 2\sqrt{5} \text{ cm}
3. Tính diện tích xung quanh S :
A = \pi \cdot 2 \cdot 2\sqrt{5} = 4\pi\sqrt{5} \text{ cm}^2 \approx 17.78 \text{ cm}^2
Kết Luận
Diện tích xung quanh hình nón là khái niệm quan trọng trong hình học. Hiểu được cách tính diện tích xung quanh giúp bạn áp dụng vào thực tế và giải quyết các bài toán trong học tập.
Thông qua bài viết này, bạn đã nắm được định nghĩa, công thức tính, cũng như một số bài tập từ cơ bản đến nâng cao liên quan đến diện tích xung quanh hình nón. Hy vọng những kiến thức này sẽ hữu ích cho bạn trong quá trình học tập toán học!
