Tính Diện tích xung quanh hình trụ tròn Online – Công thức chuẩn

Hình trụ tròn là một trong những hình khối phổ biến trong hình học không gian. Trong bài viết này, chúng ta sẽ tìm hiểu về khái niệm, công thức tính diện tích xung quanh của hình trụ tròn, cùng với một số bài tập từ cơ bản đến nâng cao để hiểu rõ hơn về vấn đề này.

Định Nghĩa Hình Trụ Tròn

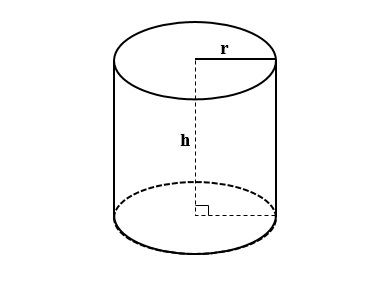
Hình trụ tròn là hình khối được tạo thành từ hai mặt tròn song song và một mặt cong nối giữa hai mặt tròn đó. Để mô tả một hình trụ tròn, bạn cần biết hai thông số quan trọng:

– Bán kính (r): Bán kính của hai mặt tròn.
– Chiều cao (h): Khoảng cách giữa hai mặt tròn.

Hình trụ tròn có nhiều ứng dụng thực tiễn trong đời sống, chẳng hạn như chai nước, ống hút, và nhiều loại vật dụng khác.

Công Thức Tính Diện Tích Xung Quanh Hình Trụ Tròn

Diện tích xung quanh của hình trụ tròn là tổng diện tích bề mặt bên ngoài của hình trụ, không bao gồm hai mặt tròn ở trên và dưới. Công thức tính diện tích xung quanh của hình trụ tròn được cho bởi:

S = 2 \pi r h

Trong đó:
– S là diện tích xung quanh của hình trụ tròn (đơn vị: cm², m², v.v.).
– r là bán kính của mặt tròn (đơn vị: cm, m, v.v.).
– h là chiều cao của hình trụ (đơn vị: cm, m, v.v.).
– \pi là một hằng số xấp xỉ bằng 3.14.

Ví Dụ Tính Diện Tích Xung Quanh

Giả sử bạn có một hình trụ tròn với bán kính r = 4 cm và chiều cao h = 10 cm. Chúng ta có thể tính diện tích xung quanh như sau:

1. Áp dụng công thức:
S = 2 \pi r h = 2 \pi \cdot 4 \cdot 10
2. Tính giá trị:
S = 80 \pi \approx 251.33 , \text{cm}^2

Một Số Bài Tập Tính Diện Tích Xung Quanh

Bài Tập Cơ Bản

Bài 1: Một hình trụ tròn có bán kính 3 cm và chiều cao 5 cm. Tính diện tích xung quanh của hình trụ này.

Giải:
– Bán kính r = 3 cm.
– Chiều cao h = 5 cm.
– Công thức:
S = 2 \pi r h = 2 \pi \cdot 3 \cdot 5 = 30 \pi \approx 94.25 , \text{cm}^2

Bài 2: Tính diện tích xung quanh của hình trụ tròn có chiều cao 8 m và bán kính 2 m.

Giải:
– Bán kính r = 2 m.
– Chiều cao h = 8 m.
– Công thức:
S = 2 \pi r h = 2 \pi \cdot 2 \cdot 8 = 32 \pi \approx 100.53 , \text{m}^2

Bài Tập Nâng Cao

Bài 3: Tính diện tích xung quanh hình trụ tròn có bán kính 7 cm và chiều cao gấp đôi chiều cao của hình trụ có bán kính 5 cm với diện tích xung quanh là 100 π cm².

Giải:

1. Tính chiều cao của hình trụ với bán kính 5 cm:

S = 100 \pi = 2 \pi \cdot 5 \cdot h

=> h = 10 \text{ cm}

2. Chiều cao của hình trụ có bán kính 7 cm là:
h' = 2h = 20 \text{ cm}

3. Tính diện tích xung quanh:
S' = 2 \pi r h' = 2 \pi \cdot 7 \cdot 20 = 280 \pi \approx 879.65 , \text{cm}^2

Kết Luận

Diện tích xung quanh của hình trụ tròn là một khái niệm cơ bản trong hình học không gian. Việc nắm vững cách tính diện tích này không chỉ giúp bạn giải quyết các bài toán trong sách giáo khoa mà còn hữu ích trong các ứng dụng thực tế như thiết kế và xây dựng. Hãy thực hành thêm với các bài tập khác để củng cố kiến thức của bạn nhé!