Tính Thể Tích Hình Bán Cầu Online Dễ dàng, Công Thức Chuẩn

Hình bán cầu là một trong những hình khối đặc biệt và có nhiều ứng dụng thực tiễn trong đời sống cũng như trong khoa học. Trong bài viết này, chúng ta sẽ cùng tìm hiểu về thể tích hình bán cầu, bao gồm định nghĩa, công thức tính toán cũng như một số bài tập từ cơ bản đến nâng cao để các bạn có thể nắm vững kiến thức này.

Định Nghĩa Hình Bán Cầu

Hình bán cầu là một hình khối được tạo thành từ một nửa của hình cầu. Nó có thể được tưởng tượng như một hình cầu được cắt đôi theo mặt phẳng đi qua tâm và vuông góc với trục. Hình bán cầu có một mặt cong – phần nửa phía trên và một mặt phẳng – phần đáy.

Đặc điểm của hình bán cầu:

– Có bán kính (r), là khoảng cách từ tâm của hình cầu đến bất kỳ điểm nào trên bề mặt của hình cầu.
– Mặt cong của hình bán cầu là hình tròn, trong khi mặt phẳng là một vòng tròn.

Công Thức Tính Thể Tích Hình Bán Cầu

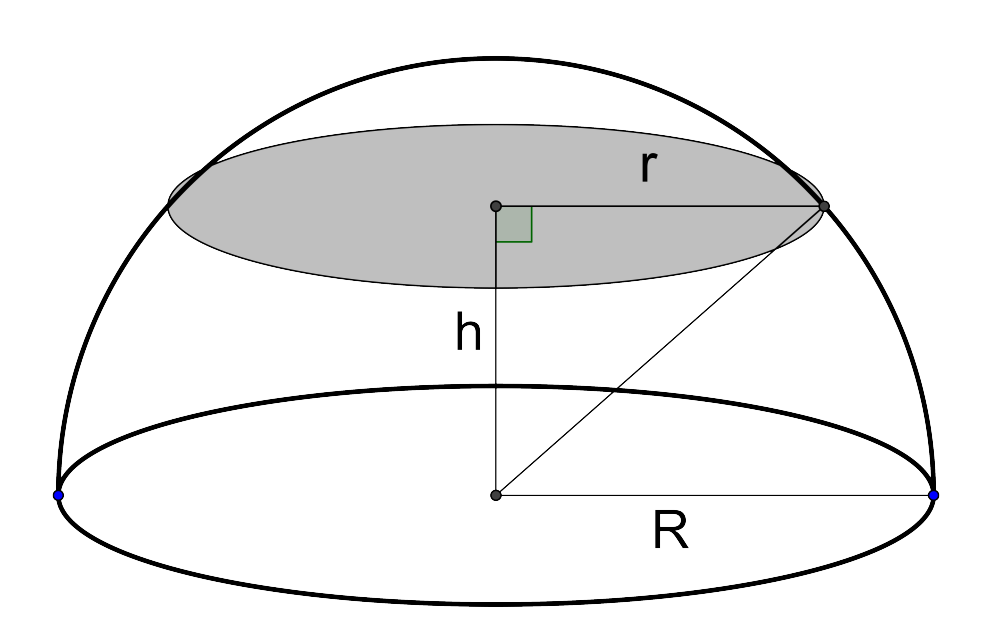
Công thức tính thể tích của hình bán cầu được tính dựa trên công thức tính thể tích của hình cầu. Thể tích của một hình cầu được tính theo công thức:

V_{cầu} = \frac{4}{3} \pi r^3

Do đó, thể tích của hình bán cầu sẽ bằng một nửa thể tích của hình cầu:

V_{bán  cầu} = \frac{1}{2} \cdot V_{cầu} = \frac{1}{2} \cdot \frac{4}{3} \pi r^3 = \frac{2}{3} \pi r^3

Trong đó:

– V_{bán  cầu} : thể tích của hình bán cầu.
– r : bán kính của hình bán cầu.
– \pi : hằng số Pi (khoảng 3.14).

Một Vài Bài Tập Về Thể Tích Hình Bán Cầu

Bài Tập 1: Tính Thể Tích Hình Bán Cầu Có Bán Kính 5 cm

Giả sử chúng ta có một hình bán cầu có bán kính là 5 cm. Để tính thể tích, chúng ta sử dụng công thức đã nêu ở trên:

V_{bán  cầu} = \frac{2}{3} \pi r^3

Thay r = 5 :

V_{bán  cầu} = \frac{2}{3} \pi \cdot 5^3 = \frac{2}{3} \pi \cdot 125 = \frac{250}{3} \pi \approx 261.8 \text{ cm}^3

Vậy thể tích của hình bán cầu này là khoảng 261.8 cm³.

Bài Tập 2: Tính Thể Tích Hình Bán Cầu Có Bán Kính 10 cm

Tiếp theo, chúng ta sẽ tính thể tích của một hình bán cầu có bán kính 10 cm.

Sử dụng lại công thức:

V_{bán  cầu} = \frac{2}{3} \pi r^3

Thay r = 10 :

V_{bán  cầu} = \frac{2}{3} \pi \cdot 10^3 = \frac{2}{3} \pi \cdot 1000 = \frac{2000}{3} \pi \approx 2093.3 \text{ cm}^3

Như vậy, thể tích hình bán cầu có bán kính 10 cm là khoảng 2093.3 cm³.

Bài Tập 3: Bài Tập Nâng Cao

Giả sử bạn có một hình cầu với bán kính là r . Tính thể tích hình bán cầu khi r có giá trị là x .

Vậy thể tích hình bán cầu sẽ là:

V_{bán  cầu} = \frac{2}{3} \pi x^3

Bài Tập 4: Ứng Dụng Trong Thực Tiễn

Một câu hỏi thú vị là: Nếu bạn có một hình bán cầu làm bằng bê tông và bạn muốn biết khả năng chứa nước của nó, hãy xem xét một hình bán cầu với bán kính là 7 m. Bạn hãy tính thể tích?

Ta có:

V_{bán  cầu} = \frac{2}{3} \pi \cdot 7^3 = \frac{2}{3} \pi \cdot 343 = \frac{686}{3} \pi \approx 719.8 \text{ m}^3

Vậy hình bán cầu này có thể chứa khoảng 719.8 m³ nước.

Kết Luận

Hình bán cầu không chỉ có ý nghĩa lý thuyết mà còn có nhiều ứng dụng thực tiễn trong xây dựng, thiết kế đồ vật và nghiên cứu khoa học. Qua bài viết này, chúng ta đã tìm hiểu về định nghĩa, công thức tính thể tích và một số bài tập mẫu. Hy vọng rằng kiến thức này sẽ giúp ích cho bạn trong việc học tập và ứng dụng vào thực tiễn!