Tính Thể Tích Hình Chóp Đều Online Dễ dàng, Công Thức Chuẩn

Hình chóp đều là một trong những khái niệm cơ bản trong hình học không gian. Trong bài viết này, chúng ta sẽ khám phá thể tích của hình chóp đều, định nghĩa, công thức tính cũng như giải quyết một vài bài tập từ cơ bản đến nâng cao để giúp bạn có cái nhìn rõ ràng hơn về khái niệm này.

Định Nghĩa Hình Chóp Đều

Hình chóp đều là một loại hình chóp mà phần đáy của nó là một đa giác đều, và các cạnh bên của nó đều nhau. Đỉnh của hình chóp nằm trực tiếp trên mặt phẳng chứa đa giác đáy, tạo thành một hình chóp có tính đối xứng rất cao.

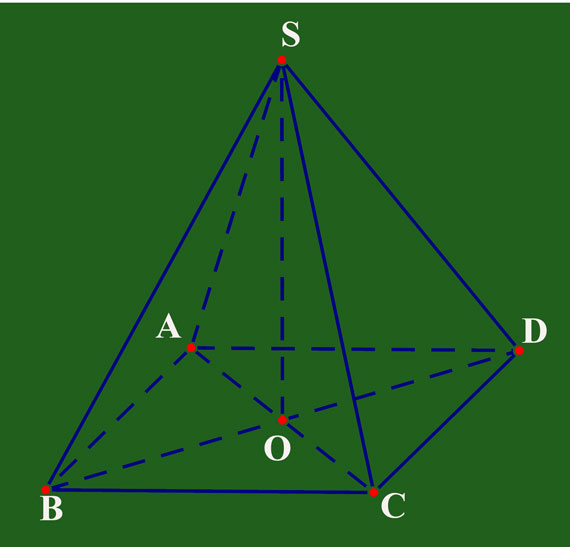
Một số Hình Chóp Đều thường gặp

– Hình chóp tam giác đều: có đáy là một tam giác đều và ba cạnh bên bằng nhau.
– Hình chóp vuông: có đáy là một hình vuông và bốn cạnh bên bằng nhau.

Công Thức Tính Thể Tích Hình Chóp Đều

Công thức tính thể tích V của một hình chóp đều với diện tích đáy S và chiều cao h được biểu diễn như sau:

V = \frac{1}{3} S h

Trong đó:
– V là thể tích của hình chóp đều.
– S là diện tích của đáy.
– h là chiều cao từ đỉnh chóp đến mặt phẳng chứa đáy.

Tính Diện Tích Đáy

Để sử dụng công thức trên, chúng ta cần biết diện tích của đáy. Diện tích của đáy phụ thuộc vào hình dạng của nó.

– Tam giác đều: Nếu đáy là một tam giác đều có cạnh dài a , diện tích được tính bằng công thức:

S = \frac{\sqrt{3}}{4} a^2

– Hình vuông: Nếu đáy là một hình vuông với cạnh dài a , thì diện tích được tính bằng:

S = a^2

Ví dụ Tính Thể Tích Hình Chóp Đều

Bài Tập Cơ Bản

Bài 1: Tính thể tích của một hình chóp tam giác đều có cạnh đáy a = 6 cm và chiều cao h = 12 cm.

1. Tính diện tích đáy:

Áp dụng công thức diện tích tam giác đều:

S = \frac{\sqrt{3}}{4} a^2 = \frac{\sqrt{3}}{4} \cdot 6^2 = \frac{\sqrt{3}}{4} \cdot 36 = 9\sqrt{3} , \text{cm}^2

2. Tính thể tích:

Áp dụng công thức thể tích:

V = \frac{1}{3} S h = \frac{1}{3} \cdot 9\sqrt{3} \cdot 12 = 36\sqrt{3} , \text{cm}^3

Bài Tập Nâng Cao

Bài 2: Một hình chóp vuông có cạnh đáy a = 10 cm và chiều cao h = 15 cm. Tính thể tích của hình chóp này.

1. Tính diện tích đáy:

S = a^2 = 10^2 = 100 , \text{cm}^2

2. Tính thể tích:

V = \frac{1}{3} S h = \frac{1}{3} \cdot 100 \cdot 15 = 500 , \text{cm}^3

Bài Tập Khó

Bài 3: Một hình chóp đều có đáy là một hình vuông với cạnh đáy dài a = 8 cm. Chiều cao của chóp là h = 10 cm. Tính thể tích và độ dài cạnh bên của hình chóp.

1. Tính diện tích đáy:

S = a^2 = 8^2 = 64 , \text{cm}^2

2. Tính thể tích:

V = \frac{1}{3} S h = \frac{1}{3} \cdot 64 \cdot 10 = \frac{640}{3} , \text{cm}^3 \approx 213.33 , \text{cm}^3

3. Tính độ dài cạnh bên:

Chúng ta sử dụng định lý Pythagoras. Độ dài cạnh bên l được tính bằng công thức:

l = \sqrt{\left(\frac{a}{2}\right)^2 + h^2} = \sqrt{\left(\frac{8}{2}\right)^2 + 10^2} = \sqrt{4^2 + 10^2} = \sqrt{16 + 100} = \sqrt{116} \approx 10.77 , \text{cm}

Kết Luận

Như vậy, chúng ta đã cùng tìm hiểu về thể tích hình chóp đều, từ định nghĩa, công thức tới những bài tập thực tiễn. Việc nắm vững khái niệm và áp dụng chính xác sẽ giúp bạn giải quyết các bài toán liên quan đến hình khối trong hình học không gian. Nếu bạn có bất kỳ câu hỏi nào, đừng ngần ngại để lại ý kiến dưới bài viết này!