Tính Thể Tích Hình Lăng Trụ Tam Giác Online – Công Thức Chuẩn

Hình lăng trụ tam giác là một trong những khối hình học cơ bản thường gặp trong toán học và ứng dụng thực tiễn. Trong bài viết này, chúng ta sẽ cùng tìm hiểu định nghĩa, công thức tính thể tích của hình lăng trụ tam giác, và làm một số bài tập từ cơ bản đến nâng cao.

Định Nghĩa Hình Lăng Trụ Tam Giác

Hình lăng trụ tam giác là một khối đa diện có hai đáy hình tam giác và ba mặt bên hình chữ nhật. Tất cả các cạnh tương ứng của hai đáy là song song và cùng chiều với nhau. Hình lăng trụ tam giác được đặc trưng bởi các yếu tố sau:

– Hai đáy hình tam giác bằng nhau và song song.
– Ba mặt bên là hình chữ nhật liên kết giữa các đỉnh của đáy.

Công Thức Tính Thể Tích Hình Lăng Trụ Tam Giác

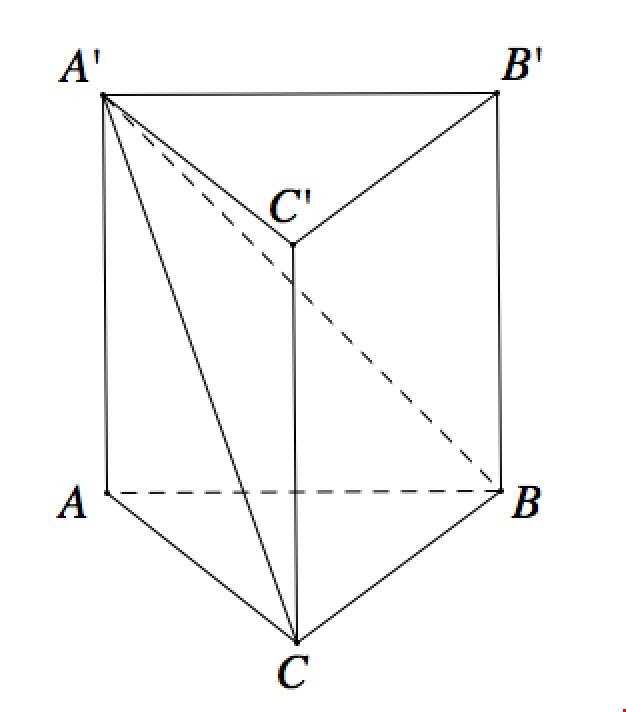
Thể tích của hình lăng trụ tam giác được tính bằng công thức:

V = S_{đáy} \cdot h

trong đó:
– V là thể tích của lăng trụ.
– S_{đáy} là diện tích đáy, tức là diện tích hình tam giác.
– h là chiều cao của lăng trụ, là khoảng cách giữa hai đáy hình tam giác.

Diện Tích Hình Tam Giác

Để tính được thể tích của lăng trụ tam giác, trước tiên chúng ta cần tính diện tích của đáy là hình tam giác. Diện tích của một hình tam giác có thể tính bằng một trong các công thức sau:

Công Thức Diện Tích Hình Tam Giác

1. Công thức Heron (đối với tam giác có ba cạnh):
S = \sqrt{p(p-a)(p-b)(p-c)}
trong đó p = \frac{a+b+c}{2} là nửa chu vi của tam giác, và a, b, c là độ dài ba cạnh.

2. Công thức theo chiều cao và đáy:
S = \frac{1}{2} \cdot b \cdot h
trong đó b là độ dài đáy của hình tam giác, và h là chiều cao tương ứng với đáy đó.

Một Số Bài Tập Tính Thể tích Hình Lăng Trụ

Để hiểu rõ hơn về cách áp dụng công thức, hãy cùng thực hiện một số bài tập.

Bài Tập 1: Tính Thể Tích Hình Lăng Trụ Tam Giác Cơ Bản

Một hình lăng trụ tam giác có đáy là hình tam giác đều với mỗi cạnh dài 6 cm và chiều cao của lăng trụ là 10 cm.

Bước 1: Tính diện tích đáy ( S_{đáy} ):
– Đối với hình tam giác đều, diện tích được tính bằng:
S = \frac{1}{4} \sqrt{3} a^2
với a = 6 :
S = \frac{1}{4} \sqrt{3} \cdot 6^2 = \frac{1}{4} \sqrt{3} \times 36 = 9\sqrt{3} \text{ cm}^2

Bước 2: Tính thể tích ( V ):
V = S_{đáy} \cdot h = 9\sqrt{3} \cdot 10 = 90\sqrt{3} \text{ cm}^3

Bài Tập 2: Tính Thể Tích với Công Thức Heron

Một hình lăng trụ tam giác có đáy là tam giác có ba cạnh lần lượt là 5 cm, 12 cm và 13 cm, chiều cao của lăng trụ là 15 cm.

Bước 1: Tính diện tích đáy:
– Tính nửa chu vi:
p = \frac{5 + 12 + 13}{2} = 15 \text{ cm}

– Tính diện tích bằng công thức Heron:
S = \sqrt{15(15-5)(15-12)(15-13)} = \sqrt{15 \cdot 10 \cdot 3 \cdot 2} = \sqrt{90 \cdot 15} = \sqrt{1350} = 30\sqrt{3} \text{ cm}^2

Bước 2: Tính thể tích:
V = S_{đáy} \cdot h = 30\sqrt{3} \cdot 15 = 450\sqrt{3} \text{ cm}^3

Bài Tập Nâng Cao

Nếu chúng ta có một lăng trụ với chiều cao 20 cm và diện tích đáy là hình tam giác có diện tích 24 cm², hãy tính thể tích.

Áp dụng công thức:
V = S_{đáy} \cdot h = 24 \cdot 20 = 480 \text{ cm}^3

Kết Luận

Chúng ta vừa tìm hiểu định nghĩa, công thức và áp dụng vào một số bài tập tính thể tích của hình lăng trụ tam giác. Hy vọng qua bài viết, bạn đã có thêm kiến thức hữu ích và áp dụng tốt trong công việc học tập cũng như giải quyết các bài toán trong thực tiễn.

Nếu bạn có thắc mắc gì, đừng ngần ngại để lại câu hỏi dưới bài viết này!