Tính Thể Tích Hình Lập Phương Online – Công Thức Chuẩn

Trong toán học, hình học là một lĩnh vực quan trọng liên quan đến các hình dạng và thể tích của chúng. Một trong những hình cơ bản và đơn giản nhất trong hình học chính là hình lập phương. Bài viết này sẽ giúp bạn tìm hiểu về thể tích hình lập phương, từ định nghĩa, công thức tính cho đến một vài bài tập từ cơ bản đến nâng cao.

Định Nghĩa Hình Lập Phương

Hình lập phương là một hình khối đặc biệt có 6 mặt, mỗi mặt là một hình vuông. Tất cả các cạnh của hình lập phương đều có độ dài bằng nhau. Gọi độ dài cạnh của hình lập phương là a . Hình lập phương có 8 đỉnh, 12 cạnh và 6 mặt. Mỗi mặt của hình lập phương đều có diện tích bằng nhau, vì vậy việc tính toán không gian mà nó chiếm trong không gian ba chiều là rất quan trọng.

Công Thức Tính Thể Tích Hình Lập Phương

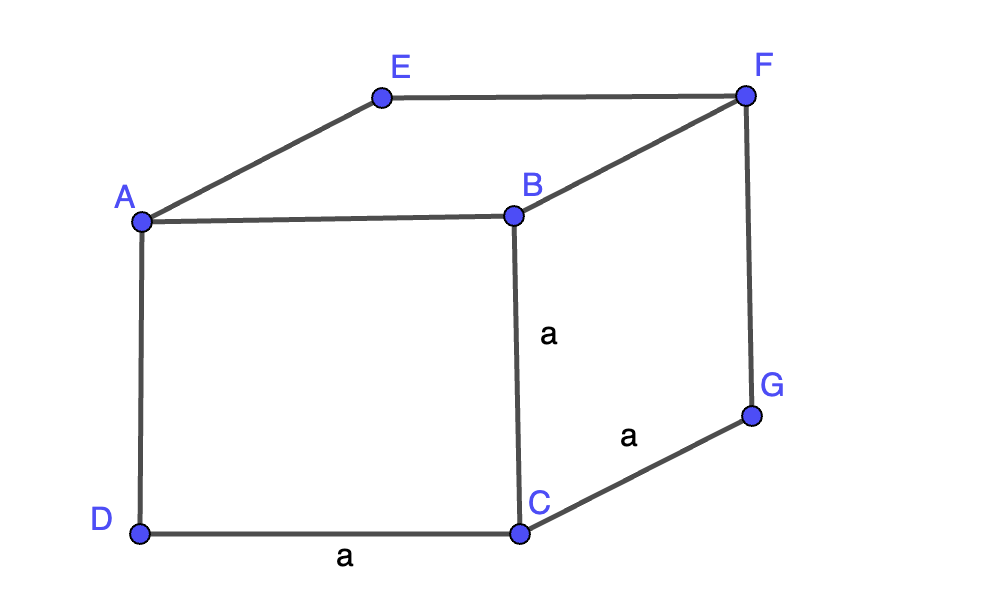
Thể tích của hình lập phương được tính bằng công thức đơn giản sau:

V = a^3

Trong đó:
– V là thể tích của hình lập phương.
– a là độ dài của một cạnh của hình lập phương.

Giải thích công thức

Công thức này dựa trên thực tế rằng để tìm thể tích của một hình khối, bạn cần nhân chiều dài, chiều rộng và chiều cao. Trong trường hợp của hình lập phương, chiều dài, chiều rộng và chiều cao đều bằng nhau và bằng a . Vì vậy, thể tích được tính bằng bình phương diện tích một mặt của hình lập phương và nhân với chiều cao (cũng chính là a trong trường hợp này).

Bài Tập Tính Thể Tích Hình Lập Phương

Để hiểu rõ hơn về cách tính thể tích hình lập phương, hãy cùng làm một số bài tập từ cơ bản đến nâng cao.

Bài Tập 1: Tính thể tích với cạnh bằng 5 cm

Đề bài: Tính thể tích của một hình lập phương có độ dài cạnh là 5 cm.

Giải:
Sử dụng công thức:

V = a^3

Thay a vào công thức:

V = 5^3 = 125 \text{ cm}^3

Vậy, thể tích của hình lập phương là 125 cm³.

Bài Tập 2: Tính thể tích với cạnh bằng 10 m

Đề bài: Tính thể tích của một hình lập phương có độ dài cạnh là 10 m.

Giải:
Sử dụng công thức:

V = a^3

Thay a vào công thức:

V = 10^3 = 1000 \text{ m}^3

Vậy, thể tích của hình lập phương là 1000 m³.

Bài Tập 3: So sánh thể tích hai hình lập phương khác nhau

Đề bài: Tính thể tích của hai hình lập phương, một có cạnh là 4 cm và cái còn lại có cạnh là 6 cm. So sánh thể tích của hai hình lập phương này.

Giải:
– Đầu tiên, tính thể tích của hình lập phương thứ nhất:

V_1 = 4^3 = 64 \text{ cm}^3

– Tiếp theo, tính thể tích của hình lập phương thứ hai:

V_2 = 6^3 = 216 \text{ cm}^3

– So sánh hai thể tích:
V_1 < V_2

Vậy, hình lập phương có cạnh 6 cm có thể tích lớn hơn hình lập phương có cạnh 4 cm.

Bài Tập 4: Tìm cạnh hình lập phương từ thể tích đã biết

Đề bài: Một hình lập phương có thể tích là 729 cm³. Tính độ dài cạnh của hình lập phương này.

Giải:
Sử dụng công thức thể tích:

V = a^3

Với V = 729 \text{ cm}^3 , ta có:

a^3 = 729

Để tìm a , ta lấy căn bậc ba của 729:

a = \sqrt[3]{729} = 9 \text{ cm}

Vậy, độ dài cạnh của hình lập phương là 9 cm.

Bài Tập 5: Thể tích hình lập phương trong các bài toán thực tế

Đề bài: Một hình lập phương có độ dài cạnh 3 m. Tính thể tích và nếu bạn muốn chứa nước trong đó, nó có thể chứa bao nhiêu lít nước (biết 1 m³ nước = 1000 lít)?

Giải:
Đầu tiên, tính thể tích:

V = 3^3 = 27 \text{ m}^3

Chuyển đổi sang lít:

Vậy, thể tích nước chứa được là:

27 \text{ m}^3 = 27 \times 1000 = 27000 \text{ lít}

Kết Luận

Hình lập phương là một hình khối rất quen thuộc trong toán học với thể tích dễ dàng tính toán thông qua công thức đơn giản. Việc giải các bài tập từ cơ bản đến nâng cao giúp bạn nắm vững hơn về kiến thức này. Hy vọng bài viết này đã mang đến cho bạn cái nhìn tổng quan về thể tích hình lập phương và cách áp dụng nó trong các tình huống thực tiễn. Nếu bạn còn thắc mắc gì, hãy để lại câu hỏi bên dưới nhé!