Tính Thể Tích Hình Nón Cụt Online Nhanh Chóng, Công Thức Chuẩn

Hình nón cụt là một trong những hình học không gian quan trọng trong toán học. Nó không chỉ xuất hiện trong lý thuyết mà còn có ứng dụng thực tế trong đời sống. Trong bài viết này, chúng ta sẽ tìm hiểu về thể tích của hình nón cụt, định nghĩa, công thức tính thể tích, và một số bài tập từ cơ bản đến nâng cao để bạn nắm vững kiến thức này.

Định nghĩa hình nón cụt

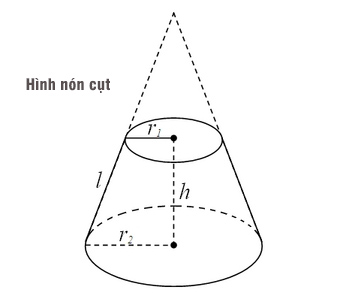
Hình nón cụt là một khối hình được tạo bởi hai mặt hình tròn nối với nhau bằng một mặt phẳng cong. Hình nón cụt thường được mô tả bằng các yếu tố sau:

– Cạnh bên: Là đoạn thẳng nối từ đỉnh của nón (thường bị cắt) đến các điểm trên đường tròn đáy.
– Đáy lớn (r1) và đáy nhỏ (r2): Là bán kính của hai mặt đáy của hình nón cụt.
– Chiều cao (h): Là khoảng cách vuông góc giữa hai đáy của hình nón cụt.

Hình nón cụt có thể tưởng tượng như là hình nón bị cắt bởi một mặt phẳng song song với đáy.

Công thức tính thể tích hình nón cụt

Để tính thể tích của hình nón cụt, ta sử dụng công thức sau:

V = \frac{1}{3} \pi h (r_1^2 + r_1 r_2 + r_2^2) 

Trong đó:
– V là thể tích hình nón cụt.
– h là chiều cao của hình nón cụt.
– r_1 là bán kính đáy lớn.
– r_2 là bán kính đáy nhỏ.
– \pi là hằng số Pi, khoảng 3.14.

Bài tập tính thể tích hình nón cụt

Bài tập 1: Tính thể tích hình nón cụt cơ bản

Đề bài: Một hình nón cụt có đáy lớn bán kính r_1 = 5 cm, đáy nhỏ bán kính r_2 = 3 cm và chiều cao h = 10 cm. Tính thể tích của hình nón cụt này.

Giải:
Áp dụng công thức tính thể tích:

V = \frac{1}{3} \pi \cdot h \cdot (r_1^2 + r_1 r_2 + r_2^2) 

Thay các giá trị vào công thức:

V = \frac{1}{3} \pi \cdot10 \cdot (5^2 + 5 \cdot 3 + 3^2)

= \frac{1}{3} \pi \cdot 10 \cdot (25 + 15 + 9)
= \frac{1}{3} \pi \cdot 10 \cdot 49
= \frac{490}{3} \pi
\approx 513.13 \text{ cm}^3

Bài tập 2: Bài toán nâng cao

Đề bài: Một hình nón cụt có đáy lớn bán kính r_1 = 4 m, đáy nhỏ bán kính r_2 = 2 m và chiều cao h = 6 m. Tính thể tích của hình nón cụt này và làm tròn kết quả đến hai chữ số thập phân.

Giải:
Sử dụng công thức:
V = \frac{1}{3} \pi \cdot h \cdot (r_1^2 + r_1 r_2 + r_2^2)

Thay vào công thức:
V = \frac{1}{3} \pi \cdot 6 \cdot (4^2 + 4 \cdot 2 + 2^2)
= \frac{1}{3} \pi \cdot 6 \cdot (16 + 8 + 4)
= \frac{1}{3} \pi \cdot 6 \cdot 28  
= 56 \pi
Giá trị xấp xỉ:
V \approx 56 \times 3.14 \approx 175.84 \text{ m}^3

Bài tập 3: Ứng dụng trong thực tế

Đề bài: Một chiếc chậu hình nón cụt có đáy lớn bán kính 15 cm, đáy nhỏ bán kính 10 cm và chiều cao 20 cm. Tính thể tích chậu để biết nó có thể chứa được bao nhiêu lít nước (biết 1 [latex] lít = [latex] 1000 cm³).

Giải:
Áp dụng công thức:
V = \frac{1}{3} \pi \cdot 20 \cdot (15^2 + 15 \cdot 10 + 10^2)
= \frac{1}{3} \pi \cdot 20 \cdot (225 + 150 + 100)
= \frac{1}{3} \pi \cdot20 \cdot 475
= \frac{9500}{3} \pi
Giá trị xấp xỉ:
V \approx 9950 \text{ cm}^3
Chuyển sang lít:
\frac{9950}{1000} \approx 9.95 \text{ lít}

Kết luận

Qua bài viết này, chúng ta đã tìm hiểu về thể tích của hình nón cụt, định nghĩa, công thức và cảm nhận được sự thú vị của nó thông qua những bài tập thực hành. Hy vọng rằng những thông tin và bài tập này sẽ giúp bạn nắm vững kiến thức về hình nón cụt và biết cách áp dụng vào thực tiễn một cách hiệu quả. Nếu bạn có bất kỳ câu hỏi hay thắc mắc nào, hãy để lại ý kiến của bạn ở phần bình luận bên dưới!