Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
Hình nón là một trong những hình khối cơ bản trong hình học không gian. Bài viết này sẽ giúp bạn hiểu rõ về thể tích hình nón, bao gồm định nghĩa, công thức tính toán và một số bài tập từ cơ bản đến nâng cao.
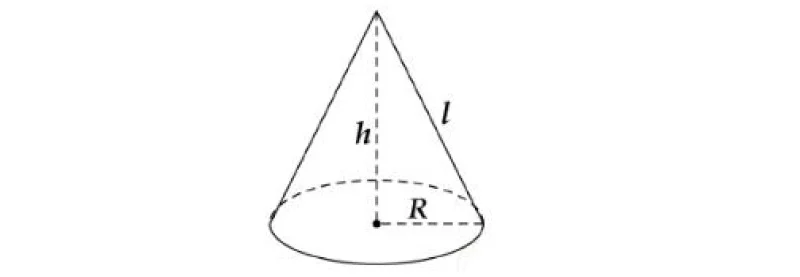
Hình nón là một khối hình không gian có một mặt đáy là một hình tròn và một đỉnh nằm bên trên mặt đáy. Mặt bên của hình nón được tạo thành từ các đoạn thẳng nối từ điểm đỉnh đến các điểm trên đường tròn đáy. Hình nón được mô tả bằng ba thông số chính: bán kính đáy (r), chiều cao (h) và đường kính (d).
– Bán kính đáy (r): Là bán kính của đường tròn đáy của hình nón.
– Chiều cao (h): Là đoạn thẳng vuông góc từ đỉnh của hình nón đến mặt đáy.
– Đường sinh (l): Là đoạn thẳng nối từ đỉnh đến điểm bất kỳ trên đường tròn đáy.
Từ các thông số này, chúng ta có thể tính được thể tích của hình nón.
Công thức tính thể tích V của hình nón được cho bởi:
V = \frac{1}{3} \pi r^2 hTrong đó:
– V là thể tích của hình nón.
– r là bán kính đáy.
– h là chiều cao của hình nón.
– \pi là hằng số Pi, khoảng 3.14.
Công thức này thể hiện rằng thể tích của hình nón bằng một phần ba thể tích của hình trụ có cùng bán kính và chiều cao.
Bài tập 1: Tính thể tích của hình nón có bán kính đáy r = 3 cm và chiều cao h = 4 cm.
Giải:
Áp dụng công thức trên:
– Bán kính (r) = 3 cm
– Chiều cao (h) = 4 cm
Tính thể tích:
V = \frac{1}{3} \pi (3)^2 (4) = \frac{1}{3} \pi (9)(4) = \frac{36\pi}{3} = 12\pi \approx 37.68 \text{ cm}^3Bài tập 2: Một hình nón có chiều cao 10 cm và bán kính đáy 5 cm. Tính thể tích của hình nón đó.
Giải:
Áp dụng công thức:
– Bán kính (r) = 5 cm
– Chiều cao (h) = 10 cm
Tính thể tích:
V = \frac{1}{3} \pi (5)^2 (10) = \frac{1}{3} \pi (25)(10) = \frac{250\pi}{3} \approx 261.8 \text{ cm}^3Bài tập 3: Một hình nón có thể tích là 100 cm³ và chiều cao là 6 cm. Hãy tính bán kính đáy của hình nón.
Giải:
Áp dụng công thức và giải cho r:
V = \frac{1}{3} \pi r^2 h
=> 100 = \frac{1}{3} \pi r^2 (6)
=> 100 = 2\pi r^2
=> r^2 = \frac{100}{2\pi} \Rightarrow r = \sqrt{\frac{100}{2\pi}} \approx 5.64 \text{ cm}
1. Tính thể tích hình nón với bán kính và chiều cao cho trước.
2. Giải bài toán liên quan đến thể tích và các thông số khác.
3. Áp dụng tìm bán kính hoặc chiều cao của hình nón khi biết thể tích.
Thể tích hình nón là một khái niệm quan trọng trong hình học không gian. Việc hiểu rõ công thức và cách áp dụng nó để giải quyết các bài toán sẽ giúp bạn có nền tảng vững chắc trong Toán học. Hãy thực hành nhiều bài tập để cải thiện kỹ năng của mình! Nếu bạn có bất kỳ câu hỏi nào về thể tích hình nón hoặc các khái niệm liên quan, hãy để lại comment bên dưới để được hỗ trợ.